题目内容
10.已知在△ABC中,三个内角A、B、C的对边分别为a、b、c,三边a、b、c依次成等差数列.(1)求证:$\frac{b}{c}$=$\frac{2}{3}$(2-cosA);
(2)若A=$\frac{2π}{3}$,求a:b:c.
分析 (1)由a、b、c依次成等差数列得到2b=a+c,利用余弦定理把等式右边化为仅含有边的代数式,然后利用分析法证明等式;
(2)把A=$\frac{2π}{3}$代入$\frac{b}{c}$=$\frac{2}{3}$(2-cosA),整理得到$\frac{b}{c}=\frac{5}{3}$,结合2b=a+c得到$\frac{a}{b}=\frac{7}{5}$,进一步求得a:b:c.
解答 (1)证明:∵a、b、c依次成等差数列,∴2b=a+c,
∵$\frac{2}{3}$(2-cosA)=$\frac{2}{3}(2-\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc})$=$\frac{2}{3}•\frac{4bc-{b}^{2}-{c}^{2}+{a}^{2}}{2bc}=\frac{4bc-{b}^{2}-{c}^{2}+{a}^{2}}{3bc}$.
∴要证$\frac{b}{c}$=$\frac{2}{3}$(2-cosA),只要证$\frac{b}{c}=\frac{4bc-{b}^{2}-{c}^{2}+{a}^{2}}{3bc}$,
即证3b2=4bc-b2-c2+a2,也就是证:4bc-4b2-c2+a2=0.
∵2b=a+c,∴4bc-4b2-c2+a2=(2a+2c)c-(a+c)2-c2-a2=2ac+2c2-a2-2ac-2c2+a2=0.
∴$\frac{b}{c}$=$\frac{2}{3}$(2-cosA);
(2)∵A=$\frac{2π}{3}$,且$\frac{b}{c}$=$\frac{2}{3}$(2-cosA),
∴$\frac{b}{c}=\frac{2}{3}(2-cos\frac{2π}{3})=\frac{2}{3}(2+\frac{1}{2})=\frac{5}{3}$,
又2b=a+c,∴$2b=a+\frac{3}{5}b$,即$\frac{7}{5}b=a$,$\frac{a}{b}=\frac{7}{5}$.
∴a:b:c=7:5:3.
点评 本题考查等差数列的性质,考查了余弦定理在解三角形中的应用,训练了利用分析法证明等式,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 2∈A | B. | 3∉A | C. | -1∈A | D. | 1∈A |
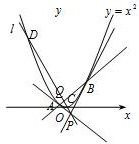 如图所示,已知过一点P(1,-1)作抛物线y=x2的两条切线,切点分别为A、B;过点P的直线l与抛物线y=x2和线段AB分别相交于两点C、D和点Q.
如图所示,已知过一点P(1,-1)作抛物线y=x2的两条切线,切点分别为A、B;过点P的直线l与抛物线y=x2和线段AB分别相交于两点C、D和点Q.