��Ŀ����
����Ŀ��ij�������ֳ��������ͺŵ�ˮ��Ħ�У�������ԱΪ���˽�ˮ��Ħ�е�ʹ������������ֳǴ����ľ�������������Ըó������6��ˮ��Ħ�е�ʹ�����������ͳ�ƣ��õ�����������±���
��� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
��ݴ���x | 1 | 2 | 3 | 4 | 5 | 6 |
ʹ���� | 11 | 13 | 16 | 15 | 20 | 21 |
����������������ݣ�����С���˷���ˮ��Ħ��ʹ����![]() ������ݴ���
������ݴ���![]() �����Իع鷽�̣���Ԥ������ֳ�2019��ˮ��Ħ�е�ʹ���ʣ�
�����Իع鷽�̣���Ԥ������ֳ�2019��ˮ��Ħ�е�ʹ���ʣ�
������������ˮƽ����ߣ�������ε��ϰ���Խ��Խ�࣬�����ֳ�����������չ���������½���һ��ˮ��Ħ�У����ͺ���Ҫ��Ŀǰʹ�õĢ��͡��������֣�ÿ���۸�ֱ�Ϊ1��Ԫ��![]() ��Ԫ.�����������飬ÿ��ˮ��Ħ�еĵ�ʹ��������������.���ֳ����������Ѿ���̭������ˮ��Ħ�е�ʹ������ֱ��ȡ��50������ͳ�ƣ�ʹ������������ͼ��ʾ��
��Ԫ.�����������飬ÿ��ˮ��Ħ�еĵ�ʹ��������������.���ֳ����������Ѿ���̭������ˮ��Ħ�е�ʹ������ֱ��ȡ��50������ͳ�ƣ�ʹ������������ͼ��ʾ��
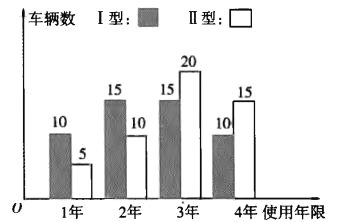
��֪ÿ��ˮ��Ħ�дӹ��뵽��̭ƽ����������![]() ��Ԫ������Ƶ����Ϊ���ʣ���ÿ��ˮ��Ħ�д���������=����-����ɱ���������ֵΪ�ο�ֵ��������ֳ��ĸ�����Ӧѡ�����ͺŵ�ˮ��Ħ�У�
��Ԫ������Ƶ����Ϊ���ʣ���ÿ��ˮ��Ħ�д���������=����-����ɱ���������ֵΪ�ο�ֵ��������ֳ��ĸ�����Ӧѡ�����ͺŵ�ˮ��Ħ�У�
�������Իع鷽��Ϊ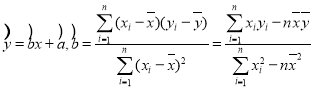 ��
��![]() ��
��
�ο����ݣ�![]()
���𰸡�����![]() ��ʹ����Ϊ
��ʹ����Ϊ![]() .����Ӧѡ�����ͺŵ�ˮ��Ħ��.
.����Ӧѡ�����ͺŵ�ˮ��Ħ��.
��������
(��)���ݹ�ʽֱ�Ӽ��㼴��.
(��)�ֱ���������ͺŵ�ˮ��Ħ��ʹ�����ĸ���,�ٷֱ�����������ѧ�����жϼ���.
�⣺�����ɱ������ݿɵ�,![]()
![]()
����ˮ��Ħ��ʹ����![]() ������ݴ���
������ݴ���![]() �����Իع鷽����
�����Իع鷽����![]()
��![]() ʱ,
ʱ,![]() ��Ԥ������ֳ�2019��ˮ��Ħ�е�ʹ����Ϊ
��Ԥ������ֳ�2019��ˮ��Ħ�е�ʹ����Ϊ![]() .
.
������Ƶ��������,�������ͼ֪����ˮ��Ħ��ÿ����ʹ��1�ꡢ2�ꡢ3���4��ĸ��ʷֱ�Ϊ![]() .
.
����ÿ������ˮ��Ħ�пɲ����Ĵ����������ֵΪ��
![]() ����Ԫ��.
����Ԫ��.
��Ƶ��������,�������ͼ֪����ˮ��Ħ��ÿ����ʹ��1�ꡢ2�ꡢ3���4��ĸ��ʷֱ�Ϊ![]() .
.
����ÿ������ˮ��Ħ�пɲ����Ĵ����������ֵΪ��
![]() ����Ԫ��.
����Ԫ��.
![]() ,����Ӧѡ�����ͺŵ�ˮ��Ħ��.
,����Ӧѡ�����ͺŵ�ˮ��Ħ��.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij���꾭��ij��Ʒ��Ϊ�˽����Ʒ��������y����λ��ǧ�������ۼ�x����λ��Ԫ/����֮��Ĺ�ϵ���ռ�5�����ݽ����˳����������õ�����������
x | 5 | 6 | 7 | 8 | 9 |
y | 8 | 6 | 4.5 | 3.5 | 3 |
��1��ͳ��ѧ�������ϵ��r��������������֮��������ع�ϵ��ǿ������![]() ������Ϊ����Ժ�ǿ����
������Ϊ����Ժ�ǿ����![]() ������Ϊ�����һ�㣻��
������Ϊ�����һ�㣻��![]() ������Ϊ����Խ���.������ϱ����ݼ���y��x֮�����ϵ��r����˵��y��x֮���������ع�ϵ��ǿ������ȷ��0.01����
������Ϊ����Խ���.������ϱ����ݼ���y��x֮�����ϵ��r����˵��y��x֮���������ع�ϵ��ǿ������ȷ��0.01����
��2����y����x�����Իع鷽�̣�
��3�����ݣ�2���е����Իع鷽�̣�Ӧ���ۼ�x��Ϊ���٣��ɻ�ȡ���������۽��������۽����������������ۼۣ�
��ע��
�ο����ݣ�![]() ��
��
�ο���ʽ�����ϵ��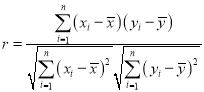 ��
��
���Իع鷽��![]() ��
�� ��
��![]() .
.