题目内容
(2011•泉州模拟)设函数f(x)=
,则方程f(x)=x的解的个数是( )
|
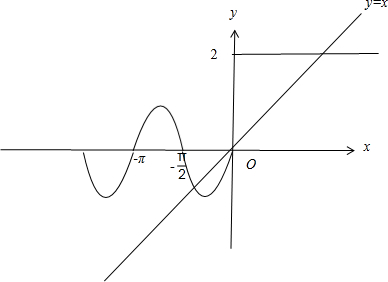
分析:我们可以在同一个直角坐标系中分别画出y=sin2x与函数y=2的图象,然后分析他们交点的个数,进行得到方程f(x)=x的根的个数,即可得到答案.
解答:解:设g(x)=x,分别作出函数y=f(x),y=g(x)的图象,如图所示
结合函数的图象可知,含y=g(x)与函数y=f(x)=
的图象有3个交点
∴方程f(x)=x的解有3个
故选C
结合函数的图象可知,含y=g(x)与函数y=f(x)=
|
∴方程f(x)=x的解有3个
故选C

点评:本题考查的知方程的根的存在性及根的个数判断,判断方程实数根的个数,即判断对应函数零点的个数,这种转化思想是解答此类问题的关键

练习册系列答案
相关题目

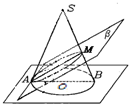 (2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )
(2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )