题目内容
(2011•泉州模拟)在区间[-2,2]任取一个实数,则该数是不等式x2>1解的概率( )
分析:根据题意先确定是几何概型中的长度类型,由不等式x2>1,则必须有x<-1或x>1,并求出构成的区域长度,再求出在区间[-2,2]上任取一个数x构成的区域长度,再求两长度的比值.
解答:解:不等式x2>1,
则有x<-1或x>1,,
即不等式x2>1,且x∈[[-2,2],则构成的区域长度为:2,
在区间[-2,2]上任取一个数x构成的区域长度为4,
使得不等式x2>1成立的概率为
;
故选C.
则有x<-1或x>1,,
即不等式x2>1,且x∈[[-2,2],则构成的区域长度为:2,
在区间[-2,2]上任取一个数x构成的区域长度为4,
使得不等式x2>1成立的概率为
| 1 |
| 2 |
故选C.
点评:本题主要考查概率的建模和解模能力,本题是长度类型,思路是先求得试验的全部构成的长度和构成事件的区域长度,再求比值.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目

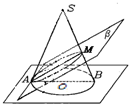 (2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )
(2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )