题目内容
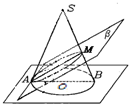 (2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )
(2011•泉州模拟)如图所示,圆锥SO的轴截面△SAB是边长为4的正三角形,M为母线SB的中点,过直线AM作平面β⊥面SAB,设β与圆锥侧面的交线为椭圆C,则椭圆C的短半轴为( )分析:过C作平行于圆锥底面的截面(圆形),交AS、BS于R、T,交椭圆C于两点P、Q,则P、Q即是椭圆短半轴顶点,先利用轴截面△SAB是边长为4的正三角形,C为AM的中点,计算RC,TC的值,再利用相交弦定理即可求得.
解答: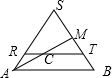 解:过椭圆C作平行于圆锥底面的截面(圆形),交AS、BS于R、T,交椭圆C于两点P、Q,则P、Q即是椭圆短半轴顶点
解:过椭圆C作平行于圆锥底面的截面(圆形),交AS、BS于R、T,交椭圆C于两点P、Q,则P、Q即是椭圆短半轴顶点
在所作的圆中,RT为直径,如图,
∵轴截面△SAB是边长为4的正三角形,C为AM的中点
∴TC=
AB=2,RC=
AB=1,
∵PQ⊥RT,∴PC=CQ
∴利用相交弦定理可得:PC×CQ=TC×RC
∴PC=
∴椭圆C的短半轴为
故选A.
 解:过椭圆C作平行于圆锥底面的截面(圆形),交AS、BS于R、T,交椭圆C于两点P、Q,则P、Q即是椭圆短半轴顶点
解:过椭圆C作平行于圆锥底面的截面(圆形),交AS、BS于R、T,交椭圆C于两点P、Q,则P、Q即是椭圆短半轴顶点在所作的圆中,RT为直径,如图,
∵轴截面△SAB是边长为4的正三角形,C为AM的中点
∴TC=
| 1 |
| 2 |
| 1 |
| 4 |
∵PQ⊥RT,∴PC=CQ
∴利用相交弦定理可得:PC×CQ=TC×RC
∴PC=
| 2 |
∴椭圆C的短半轴为
| 2 |
故选A.
点评:本题以圆锥为载体,考查圆锥的截面问题,考查椭圆的性质,解题的关键是确定椭圆短半轴顶点.

练习册系列答案
相关题目
