题目内容
19.已知关于x的方程${log_2}({4^x}+1)=x+a$有两个不同实数解,则实数a的取值范围为( )| A. | (-∞,0) | B. | (-1,2) | C. | (1,+∞) | D. | [1,+∞) |
分析 由参数分离可得2a=2x+2-x,由f(x)=2x+2-x,可得f(x)为偶函数,运用基本不等式,即可得到a的范围.
解答 解:关于x的方程${log_2}({4^x}+1)=x+a$有两个不同实数解,
即有2x+a=4x+1,即2a=2x+2-x,
由f(x)=2x+2-x,f(-x)=2-x+2x=f(x),
f(x)为偶函数,
又f(x)≥2$\sqrt{{2}^{x}•{2}^{-x}}$=2,
当且仅当x=0时,取得等号.
则有2a>2,解得a>1.
故选C.
点评 本题考查函数和方程的转化思想,考查函数的奇偶性和基本不等式的运用,属于中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
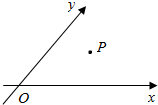 如图,设α∈(0,π)且$α≠\frac{π}{2}$,当∠xOy=α时,定义平面坐标系xOy为斜坐标系,在斜坐标系中,任意一点P的斜坐标这样定义:e1,e2分别为x轴、y轴正方向相同的单位向量,若$\overrightarrow{OP}=x{e_1}+y{e_2}$,则记为$\overrightarrow{OP}=(x,y)$,那么在以下的结论中,正确的有(2)(4)(填上所有正确结论的序号).
如图,设α∈(0,π)且$α≠\frac{π}{2}$,当∠xOy=α时,定义平面坐标系xOy为斜坐标系,在斜坐标系中,任意一点P的斜坐标这样定义:e1,e2分别为x轴、y轴正方向相同的单位向量,若$\overrightarrow{OP}=x{e_1}+y{e_2}$,则记为$\overrightarrow{OP}=(x,y)$,那么在以下的结论中,正确的有(2)(4)(填上所有正确结论的序号).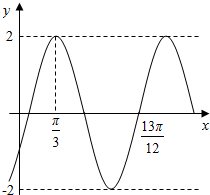 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示.