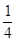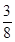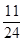题目内容
某学校组织演讲比赛，准备从甲、乙等8名学生中选派4名学生参加，要求甲、乙两名同学至少有一人参加，且若甲、乙同时参加时，他们的演讲顺序不能相邻，那么不同的演讲顺序的种数为（ ）
| A．1860 | B．1320 | C．1140 | D．1020 |
C
解析试题分析：若有甲无乙，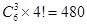
；若有乙无甲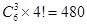，；若甲乙都有，
；所以共有
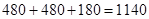.选C.
考点：排列组合.
练习册系列答案
相关题目
在
的展开式中，x的幂指数是整数的项共有
| A．3项 | B．4项 | C．5项 | D．6项 |
如果小明在某一周的第一天和第七天分别吃了3个水果，且从这周的第二天开始，每天所吃水果的个数与前一天相比，仅存在三种可能：或“多一个”或“持平”或“少一个”，那么，小明在这一周中每天所吃水果个数的不同选择方案共有（ ）
| A．50种 | B．51种 | C．140种 | D．141种 |
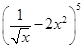的展开式中常数项是（ ）
| A．5 | B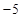． | C．10 | D． |
数列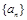
共有12项，其中
，
，
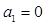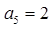，且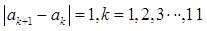
，则满足这种条件的不同数列的个数为（ ）
| A．84 | B．168 | C．76 | D．152 |
在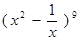
的二项式展开式中，常数项是( )
A． | B． |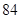
C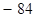． | D． |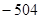
用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数的个数为( )
| A．11 | B．12 | C．13 | D．14 |
6位选手依次演讲，其中选手甲不在第一个也不在最后一个演讲，则不同的演讲次序共有( )．
| A．240种 | B．360种 | C．480种 | D．720种 |