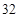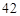题目内容
如果小明在某一周的第一天和第七天分别吃了3个水果,且从这周的第二天开始,每天所吃水果的个数与前一天相比,仅存在三种可能:或“多一个”或“持平”或“少一个”,那么,小明在这一周中每天所吃水果个数的不同选择方案共有( )
| A.50种 | B.51种 | C.140种 | D.141种 |
D
解析试题分析:小明共有6次选择,因为第一天和第七天均吃3个水果,所以在这6次选择中“多一个”和“少一个”的次数应相同、“持平”次数为偶数。当6次选择均为“持平”时,共有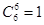 种方案;当6次选择中有4次“持平”时,选择“多一个”和“少一个”各一次,共有
种方案;当6次选择中有4次“持平”时,选择“多一个”和“少一个”各一次,共有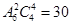 种方案;当6次选择中有2次“持平”时,选择“多一个”和“少一个”各2次,共有
种方案;当6次选择中有2次“持平”时,选择“多一个”和“少一个”各2次,共有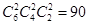 种方案;当6次选择中有0次“持平”时,选择“多一个”和“少一个”各3次,共有
种方案;当6次选择中有0次“持平”时,选择“多一个”和“少一个”各3次,共有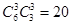 种方案.综上可得小明在这一周中每天所吃水果个数的不同选择方案共有
种方案.综上可得小明在这一周中每天所吃水果个数的不同选择方案共有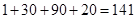 种方案,故D正确.
种方案,故D正确.
考点:排列组合,考查分类讨论思想.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
 展开式中常数项为( )
展开式中常数项为( )
A. | B. | C. | D. |
设 为整数
为整数 ,若
,若 和
和 被
被 除得的余数相同,则称
除得的余数相同,则称 和
和 对
对 同余记为
同余记为 ,已知
,已知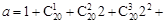 …
… ,
,  ,则
,则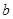 的值可以是
的值可以是
| A.2013 | B.2012 | C.2011 | D.2010 |
某学校组织演讲比赛,准备从甲、乙等8名学生中选派4名学生参加,要求甲、乙两名同学至少有一人参加,且若甲、乙同时参加时,他们的演讲顺序不能相邻,那么不同的演讲顺序的种数为( )
| A.1860 | B.1320 | C.1140 | D.1020 |
设三位数 ,若以
,若以 为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数
为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数 有( )
有( )
| A.12种 | B.24种 | C.28种 | D.36种 |
若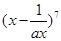 的展开式中
的展开式中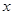 项的系数为280,则
项的系数为280,则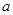 =( )
=( )
A.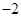 | B. | C.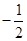 | D. |
二项式 n的展开式中各项系数的和为( ).
n的展开式中各项系数的和为( ).
| A.32 | B.-32 | C.0 | D.1 |