题目内容
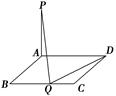
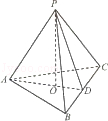
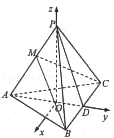
(2011•浙江)如图,在三棱锥P﹣ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
(1)证明:AP⊥BC;
(2)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.
(1)证明:AP⊥BC;
(2)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.

(1)见解析 (2)存在,3
以O为原点,以AD方向为Y轴正方向,以射线OP的方向为Z轴正方向,建立空间坐标系,
则O(0,0,0),A(0,﹣3,0),B(4,2,0),C(﹣4,2,0),P(0,0,4)
(1)则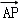 =(0,3,4),
=(0,3,4),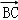 =(﹣8,0,0)
=(﹣8,0,0)
由此可得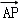 •
•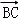 =0
=0
∴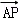 ⊥
⊥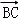
即AP⊥BC
(2)设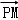 =λ
=λ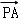 ,λ≠1,则
,λ≠1,则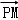 =λ(0,﹣3,﹣4)
=λ(0,﹣3,﹣4)
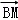 =
=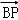 +
+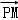 =
=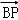 +λ
+λ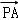 =(﹣4,﹣2,4)+λ(0,﹣3,﹣4)
=(﹣4,﹣2,4)+λ(0,﹣3,﹣4)
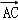 =(﹣4,5,0),
=(﹣4,5,0),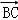 =(﹣8,0,0)
=(﹣8,0,0)
设平面BMC的法向量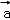 =(a,b,c)
=(a,b,c)
则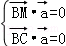
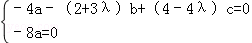
令b=1,则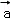 =(0,1,
=(0,1,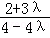 )
)
平面APC的法向量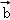 =(x,y,z)
=(x,y,z)
则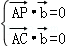
即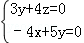
令x=5
则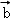 =(5,4,﹣3)
=(5,4,﹣3)
由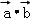 =0
=0
得4﹣3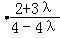 =0
=0
解得λ=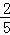
故AM=3
综上所述,存在点M符合题意,此时AM=3
则O(0,0,0),A(0,﹣3,0),B(4,2,0),C(﹣4,2,0),P(0,0,4)
(1)则
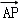 =(0,3,4),
=(0,3,4),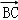 =(﹣8,0,0)
=(﹣8,0,0)由此可得
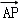 •
•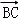 =0
=0∴
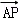 ⊥
⊥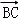
即AP⊥BC
(2)设
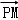 =λ
=λ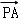 ,λ≠1,则
,λ≠1,则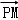 =λ(0,﹣3,﹣4)
=λ(0,﹣3,﹣4)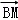 =
=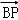 +
+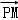 =
=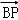 +λ
+λ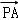 =(﹣4,﹣2,4)+λ(0,﹣3,﹣4)
=(﹣4,﹣2,4)+λ(0,﹣3,﹣4)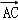 =(﹣4,5,0),
=(﹣4,5,0),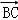 =(﹣8,0,0)
=(﹣8,0,0)设平面BMC的法向量
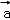 =(a,b,c)
=(a,b,c)则
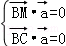
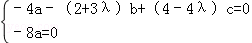
令b=1,则
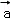 =(0,1,
=(0,1,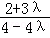 )
)平面APC的法向量
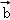 =(x,y,z)
=(x,y,z)则
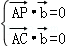
即
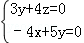
令x=5
则
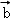 =(5,4,﹣3)
=(5,4,﹣3)由
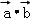 =0
=0得4﹣3
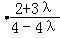 =0
=0解得λ=
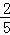
故AM=3
综上所述,存在点M符合题意,此时AM=3


练习册系列答案
相关题目

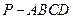 中,底面
中,底面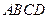 为平行四边形,
为平行四边形,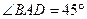 ,
,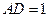 ,
,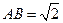 ,
,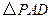 是正三角形,平面
是正三角形,平面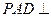 平面
平面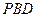 .
.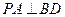 ;
;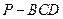 的体积.
的体积.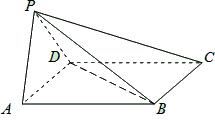
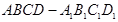 中,
中,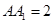 ,
,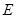 为
为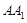 的中点,
的中点,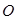 为
为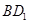 的中点.
的中点.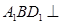 平面
平面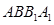 ;
;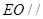 平面
平面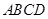 ;
;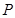 为正方体
为正方体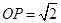 的点
的点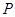 的个数,并说明理由.
的个数,并说明理由.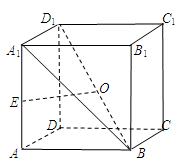
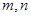 是两条不同直线,
是两条不同直线, 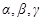 是三个不同平面,则下列正确的是( )
是三个不同平面,则下列正确的是( ) ,则
,则
 ,则
,则
 ,则
,则 ,则
,则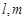 与平面
与平面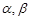 的命题中,正确的是( )
的命题中,正确的是( ) 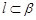 且
且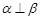 ,则
,则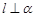
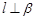 且
且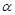 ∥
∥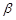 ,则
,则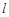 ∥
∥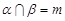 ,且
,且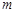 ,则
,则