题目内容
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点。
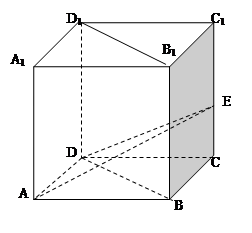
(1)求证:BD⊥AE;
(2)求点A到平面BDE的距离.

(1)求证:BD⊥AE;
(2)求点A到平面BDE的距离.
(1)详见解析,(2)

试题分析:(1)证明线线垂直,有两个思路,一是在平面几何中利用勾股定理,二是利用线面垂直转化.而异面直线垂直只能利用线面垂直转化.因为AC⊥BD,所以证明思路为证明BD⊥面ACE,而关键CC1⊥BD就可得到证明.(2)求点A到平面BDE的距离也有两个思路,一是作出A到平面BDE的距离,即垂线段,二是利用体积求高.本题作出A到平面BDE较为复杂,所以优先考虑利用体积求高.因为
 ,所以
,所以

试题解析:(1)连结AC
 ABCD-A1B1C1D1是正方体,
ABCD-A1B1C1D1是正方体, AC⊥BD,CC1⊥ABCD
AC⊥BD,CC1⊥ABCD又
 BD
BD 面ABCD,
面ABCD, CC1⊥BD
CC1⊥BD又
 AC
AC C1C=C,
C1C=C, BD⊥面ACE
BD⊥面ACE又
 AE
AE 面ACE,
面ACE, BD⊥AE
BD⊥AE(2)设A到面BDE的距离为h
 正方体的棱长为2,E为C1C中点,
正方体的棱长为2,E为C1C中点,



练习册系列答案
相关题目
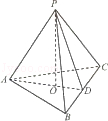
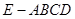 中,底面
中,底面 为正方形,
为正方形,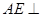 平面
平面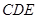 ,已知
,已知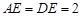 ,
,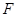 为线段
为线段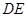 的中点.
的中点.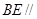 平面
平面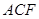 ;
;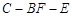 的平面角的余弦值.
的平面角的余弦值.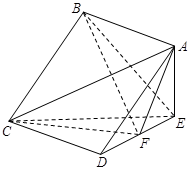
 底面ABCD,
底面ABCD,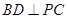 ,E是PA的中点.
,E是PA的中点.
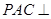 平面EBD;
平面EBD;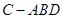 中,
中,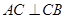 ,
,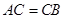 ,
,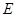 为
为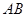 的中点,
的中点,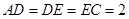 ,
,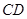 =
=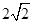 .
.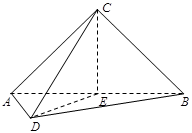
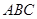 ⊥平面
⊥平面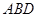 ;
;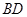 与平面
与平面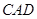 所成角的正弦值.
所成角的正弦值.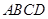 中,
中, 分别是
分别是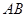 和
和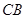 上的点,
上的点,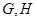 分别是
分别是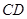 和
和 上的点,且
上的点,且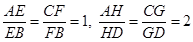 ,求证:
,求证: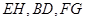 三条直线相交于同一点.
三条直线相交于同一点.
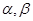 为两个不同的平面,则下列说法正确的是( )
为两个不同的平面,则下列说法正确的是( )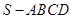 中,
中,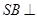 底面
底面 .底面
.底面 ,
,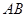 ∥
∥ ,
,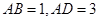 ,
, .若点
.若点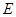 是线段
是线段 上的动点,则满足
上的动点,则满足 的点
的点
 且
且 ={直线},
={直线},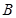 ={平面},
={平面},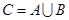 ,若
,若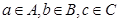 ,有四个命题①
,有四个命题①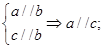 ②
②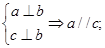 ③
③ ④
④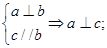 其中所有正确命题的序号是( )
其中所有正确命题的序号是( )