题目内容
如图,长方体ABCD—A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )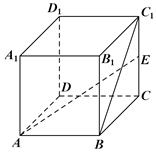
A.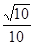 | B.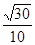 | C.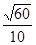 | D.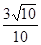 |
B
解析试题分析:连接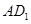 ,因为
,因为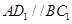 ,所以
,所以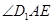 是异面直线BC1与AE所成的角,在
是异面直线BC1与AE所成的角,在 中,可以求得
中,可以求得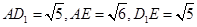 ,在三角形中,利用余弦定理可以求得角的余弦值为
,在三角形中,利用余弦定理可以求得角的余弦值为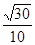 .
.
考点:本小题主要考查两条异面直线所成角的求解,考查学生的空间想象能力和推理能力.
点评:求两条异面直线所成的角,要先作出两条异面直线所成的角,要注意两条异面直线所成的角的范围.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
设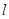 ,
,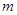 是两条不同的直线,
是两条不同的直线,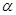 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若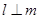 , ,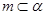 ,则 ,则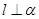 | B.若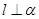 , ,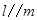 ,则 ,则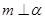 |
C.若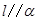 , ,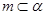 ,则 ,则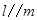 | D.若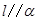 , ,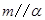 ,则 ,则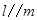 |
已知m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题正确的是 ( )
| A.若α⊥γ,α⊥β,则γ∥β | B.若m∥n,m?α,n?β,则α∥β |
| C.若m∥n,m∥α,则n∥α | D.若m∥n,m⊥α,n⊥β,则α∥β |
椭圆 的长轴为
的长轴为
 ,短轴为
,短轴为
 ,将椭圆沿y轴折成一个二面角,使得
,将椭圆沿y轴折成一个二面角,使得 点在平面
点在平面

 上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
| A.75° | B.60° | C.45° | D.30° |
若a、b表示两条不同直线,α、β表示两个不同平面,则下列命题正确的是( )
A.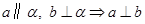 | B.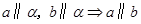 |
C.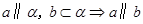 | D. |
设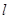 ,
,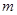 是两条不同的直线,
是两条不同的直线,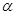 是一个平面,则下列命题正确的是 ( )
是一个平面,则下列命题正确的是 ( )
A.若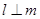 , ,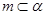 ,则 ,则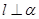 | B.若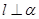 , ,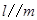 ,则 ,则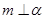 |
C.若 , ,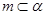 ,则 ,则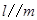 | D.若 , ,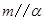 ,则 ,则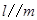 |
已知两条直线 ,
, ,两个平面
,两个平面 ,
,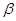 ,给出下面四个命题:
,给出下面四个命题:
①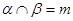 ,
,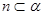
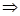
 ∥
∥ 或者
或者 ,
, 相交
相交
② ∥
∥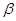 ,
, ,
,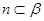
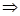
 ∥
∥
③ ∥
∥ ,
, ∥
∥
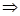
 ∥
∥
④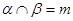 ,
,  ∥
∥
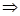
 ∥
∥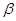 或者
或者 ∥
∥
其中正确命题的序号是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
如图长方体中,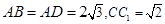 ,则二面角
,则二面角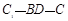 的大小为
的大小为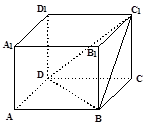
| A.300 | B.450 | C.600 | D.900 |
已知 是两条不同直线,
是两条不同直线, 是三个不同平面,下列命题正确的是( )
是三个不同平面,下列命题正确的是( )
A. |
B. |
C. |
D. |