题目内容
(1)已知椭圆以坐标轴为对称轴,且长轴是短轴的3倍,并且过点P(3,0),求椭圆的方程;
(2)已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点P1(![]() ,1)、P2(-
,1)、P2(-![]() ,-
,-![]() ),求椭圆的方程.
),求椭圆的方程.
(1)椭圆的方程为![]() 或
或![]() =1(2)
=1(2)![]()
解析:
(1)若焦点在x轴上,设方程为![]() =1 (a>b>0).
=1 (a>b>0).
∵椭圆过P(3,0),∴![]() =1.
=1.
又2a=3×2b,∴a=3,b=1,方程为![]() .
.
若焦点在y轴上,设方程为![]() =1(a>b>0).
=1(a>b>0).
∵椭圆过点P(3,0),∴![]() =1
=1
又2a=3×2b,∴a=9,b=3.∴方程为![]() =1.
=1.
∴所求椭圆的方程为![]() 或
或![]() =1.
=1.
(2)设椭圆方程为mx2+ny2=1(m>0,n>0且m≠n).
|
则 ![]()
①、②两式联立,解得![]()
∴所求椭圆方程为![]() .
.

练习册系列答案
相关题目
 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。 ,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求
,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求 的取值范围。
的取值范围。 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。 ,且
,且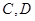 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点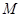 是线段
是线段 上的动点,求
上的动点,求 的取值范围。
的取值范围。 的焦点为顶点.
的焦点为顶点. 的取值范围.
的取值范围.