题目内容
已知椭圆以坐标原点为中心,坐标轴为对称轴,且椭圆以抛物线y2=16x的焦点为其一个焦点,以双曲线| x2 |
| 16 |
| y2 |
| 9 |
(1)求椭圆的标准方程;
(2)已知点A(-1,0),B(1,0),且C,D分别为椭圆的上顶点和右顶点,点P是线段CD上的动点,求
| AP |
| BP |
(3)试问在圆x2+y2=a2上,是否存在一点M,使△F1MF2的面积S=b2(其中a为椭圆的半长轴长,b为椭圆的半短轴长,F1,F2为椭圆的两个焦点),若存在,求tan∠F1MF2的值,若不存在,请说明理由.
分析:(1)先求出抛物线y2=16x的焦点和双曲线
-
=1的焦点,就可求出a,c进而求出椭圆的标准方程;
(2)先求出线段CD的方程,设出点P的坐标,找到
•
的表达式.再利用图象求出
•
的取值范围即可.
(3)先利用(1)的结论以及△F1MF2的面积求出圆的方程和点M的纵坐标,再把tan∠F1MF2的转化为两直线倾斜角的差,利用两角差的正切公式以及点M的坐标与圆的关系求出tan∠F1MF2的值即可.
| x2 |
| 16 |
| y2 |
| 9 |
(2)先求出线段CD的方程,设出点P的坐标,找到
| AP |
| BP |
| AP |
| BP |
(3)先利用(1)的结论以及△F1MF2的面积求出圆的方程和点M的纵坐标,再把tan∠F1MF2的转化为两直线倾斜角的差,利用两角差的正切公式以及点M的坐标与圆的关系求出tan∠F1MF2的值即可.
解答:解:(1)因为抛物线y2=16x的焦点和双曲线
-
=1的焦点分别为(4,0)和(5,0).
所以a=5,c=4
所以椭圆的标准方程:
+
=1;
(2)设P(x0,y0),则
•
=
+
-1;
CD:3x+5y-15=0(0≤x≤5)
则当OP⊥CD时,取到最小值,即:d1=
=
;
当P在D点时,取到最大值:OD=5
所以:
≤
•
≤24.
(3)如图所示: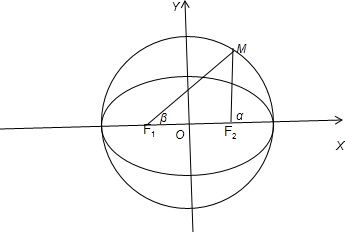
由第一问可知,圆的方程为x2+y2=25.△F1MF2的面积S=b2=9.
设M(x,y).又△F1MF2的面积S=b2=9=
×2×4×y?4y=9,
又F1(-4,0)F2(4,0).设直线MF2的倾斜角为α,直线MF1的倾斜角为β,
则tan∠F1MF2=tan(α-β)=
=
=
=
=2.
即tan∠F1MF2的值2.
| x2 |
| 16 |
| y2 |
| 9 |
所以a=5,c=4
所以椭圆的标准方程:
| x2 |
| 25 |
| y2 |
| 9 |
(2)设P(x0,y0),则
| AP |
| BP |
| x | 2 0 |
| y | 2 0 |
CD:3x+5y-15=0(0≤x≤5)
则当OP⊥CD时,取到最小值,即:d1=
| |-15| | ||
|
15
| ||
| 34 |
当P在D点时,取到最大值:OD=5
所以:
| 191 |
| 34 |
| AP |
| BP |
(3)如图所示:

由第一问可知,圆的方程为x2+y2=25.△F1MF2的面积S=b2=9.
设M(x,y).又△F1MF2的面积S=b2=9=
| 1 |
| 2 |
又F1(-4,0)F2(4,0).设直线MF2的倾斜角为α,直线MF1的倾斜角为β,
则tan∠F1MF2=tan(α-β)=
| tanα-tanβ |
| 1+tanα•tanβ |
| ||||
1+
|
| 8y |
| x2+y2-16 |
| 18 |
| 25-16 |
即tan∠F1MF2的值2.
点评:本题是对椭圆,圆,抛物线以及向量等知识的综合考查.在平时做题过程中,圆锥曲线只要出大题,一般多放在最后一题,或倒数第二题,是不易得分的题.

练习册系列答案
相关题目
 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。 ,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求
,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求 的取值范围。
的取值范围。 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。 ,且
,且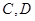 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点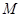 是线段
是线段 上的动点,求
上的动点,求 的取值范围。
的取值范围。 的焦点Q为顶点.
的焦点Q为顶点. 的取值范围.
的取值范围.