题目内容

2．下列函数中，在区间（0，+∞）上为增函数的是（　　）
A．y=（x-1）2B．f（x）=2-xC．y=log0.5（x+1）D．$y=\sqrt{x+1}$

分析 对选项逐个分析进行判断

解答 解：对于A，函数为二次函数，对称轴是x=1，故在（0，+∞）上不单调；
对于B，f（x）=（$\frac{1}{2}$）x，故在（0，+∞）上是减函数；
对于C，由复合函数单调性可知在（0，+∞）上为减函数；
对于D，y=（x+1）${\;}^{\frac{1}{2}}$，由复合函数单调性可知在（0，+∞）上是增函数．
故选：D．

点评 本题考查了基本初等函数的单调性，是基础题．

练习册系列答案
相关题目
12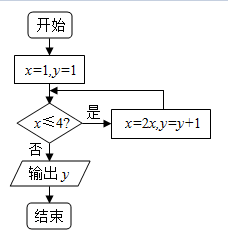．据算法语句（如图）输出的结果是（　　）
A．3B．4C．5D．8
13．关于x的方程x+log2x=[x]（[x]表示不大于x的最大整数）的解有（　　）个．
A．0B．1C．2D．3
10．已知定义域为R的函数f（x）=$\frac{{-{2^x}+b}}{{{2^{x+1}}+a}}$是奇函数．
（1）求实数a，b的值；
（2）判断函数f（x）的单调性，并说明理由；
（3）若对任意的t∈（1，4），不等式$f（4-k\sqrt{t}）+f（t）＞0$恒成立，求实数k的取值范围．
17．已知角α的终边经过点（-4，3），则sinα=$\frac{3}{5}$，cosα=-$\frac{4}{5}$．
7．已知|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=6，$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$，则$\overrightarrow a+\overrightarrow b$在$\overrightarrow a$上的投影为5．
14．已知椭圆C：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1，过E（x0，0）的直线l与椭圆C交于A，B两点，若$\frac{1}{|EA{|}^{2}}$+$\frac{1}{|EB{|}^{2}}$为定值m，则x0=$\sqrt{3}$；m=2．
11．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个顶点到两个焦点的距离分别为3+2$\sqrt{2}$，3-2$\sqrt{2}$，如果直线x=t（t∈R）与椭圆相交于不同的两点A，B，C（-3，0），D（3，0），且直线CA与直线BD的交点是K，试求点K的轨迹方程．
12．已知实数1，m，9构成一个等比数列，则圆锥曲线$\frac{{x}^{2}}{m}$+y2=1的焦距为（　　）
A．4B．2$\sqrt{2}$C．$\sqrt{2}$或2D．2$\sqrt{2}$或4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网