题目内容
【题目】如图, ![]() 为圆柱
为圆柱 ![]() 的母线,
的母线, ![]() 是底面圆
是底面圆 ![]() 的直径,
的直径, ![]() 是
是 ![]() 的中点.
的中点.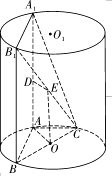
(Ⅰ)问: ![]() 上是否存在点
上是否存在点 ![]() 使得
使得 ![]() 平面
平面 ![]() ?请说明理由;
?请说明理由;
(Ⅱ)在(Ⅰ)的条件下,若 ![]() 平面
平面 ![]() ,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥
,假设这个圆柱是一个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果小鱼游到四棱锥 ![]() 外会有被捕的危险,求小鱼被捕的概率.
外会有被捕的危险,求小鱼被捕的概率.
【答案】解:(Ⅰ)存在,E是 ![]() 的中点.
的中点.
证明:如图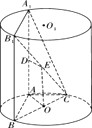
连接 ![]() ,
, ![]() ∵
∵ ![]() 分别为
分别为 ![]() ,
, ![]() 的中点,
的中点,
∴ ![]() ,
,
又 ![]() ,且
,且 ![]() ,
,
∴四边形 ![]() 是平行四边形,
是平行四边形,
即 ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
∴ ![]() 平面
平面 ![]() .
.
(Ⅱ)鱼被捕的概率 ![]() ,
,
由 ![]() 平面
平面 ![]() ,且由(Ⅰ)知
,且由(Ⅰ)知 ![]() ,∴
,∴ ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
又 ![]() 是
是 ![]() 中点,∴
中点,∴ ![]() ,因
,因 ![]() 是底面圆
是底面圆 ![]() 的直径,得
的直径,得 ![]() ,且
,且 ![]() ,
,
∴ ![]() 平面
平面 ![]() ,即
,即 ![]() 为四棱锥
为四棱锥 ![]() 的高.
的高.
设圆柱高为 ![]() ,底面半径为
,底面半径为 ![]() ,则
,则 ![]() ,
,![]() ,
,
∴ ![]() .
.
故答案为:![]() .
.
【解析】(1)要使CB1上存在点点 E 使得 DE / / 平面 ABC,则当点E为CB1的中点时,四边形 AOED 是平行四边形,能满足D E / / 平面 ABC.
(2)这是一个概型问题,由体积的比值求出概率,本题适合间接法.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
