题目内容
【题目】设函数f(x)=|x+2|﹣|x﹣1|
(I)画出函数y=f(x)的图象;
(II)若关于x的不等式f(x)+4≥|1﹣2m|有解,求实数m的取值范围.
【答案】解:(I)函数f(x)可化为:…3′
其图象如下:…5′
(II)关于x的不等式f(x)+4≥|1﹣2m|有解等价于:
(f(x)+4)max≥|1﹣2m|.…6′
由(I)可知f(x)max=3,
(也可由|f(x)|=||x+2|﹣|x﹣1||≤|(x+2)﹣(x﹣1|)|=3,得f(x)max=3)…8′
于是|1﹣2m|≤7,
解得实数m的取值范围:m∈[﹣3,4]…10′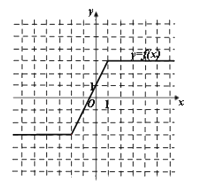
【解析】(I)先将原函数式可化为一个分段函数的形式,再分段画出函数在各段上的图象即得原函数的图象.
(II)关于x的不等式f(x)+4≥|1﹣2m|有解等价于:(f(x)+4)max≥|1﹣2m|,再根据分段函数的图象,确定函数的最大值,从而可求实数m的取值范围.
【考点精析】认真审题,首先需要了解函数的值(函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法).

 阅读快车系列答案
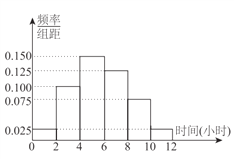
阅读快车系列答案【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
【题目】某中学将100名高一新生分成水平相同的甲、乙两个平行班,每班50人,某教师采用![]() 、
、![]() 两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.
两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.

(1)在乙班的20个个体中,从不低于86分的成绩中随机抽取2人,求抽出的两个人均“成绩优秀”的概率;
(2)由以上统计数据填写![]() 列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
甲班( | 乙班( | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |