Question

【题目】已知函数 的部分图象如图所示.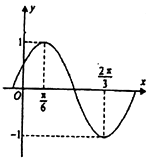

（1）求函数 的解析式，并写出 的最小正周期；
（2）令 ，若在 内，方程 有且仅有两解，求 的取值范围.

Answer 1

【答案】
（1）解：由图象可知： ，∴ ，又 ，∴ .
又∵点 在 图象上，∴ ，∴ ，
∴ ， ，又∵ ，∴ .
∴ ，最小正周期
（2）解：∵ ，
∴原方程可化为 ，则 .
∵ ， ，∴ ，
∴ ，
令 ，则 ，作出 及 图象，
当 或 时，两图象在 内有且仅有一解，
即方程 在 内有且仅有两解，
此时 的取值范围为
【解析】（1）根据图形求得函数的最小周期进而求得ω的值，再由图像上的点求得φ的值，从而求得函数的解析式；（2）先结合（1）求得函数g(x)的函数式，从而可以化简所给方程，即可用x的三角函数式子表示出a，从而将方程有且只有两解转化为两个图像有且只有两个交点的情况.