题目内容
【题目】如图,△ABC的外接圆O的直径为AB,CD⊥平面ABC,BE∥CD.

(1)求证:平面ADC⊥平面BCDE;
(2)试问在线段DE和BC上是否分别存在点M和F,使得平面OMF∥平面ACD?若存在,确定点M和点F的位置;若不存在,请说明理由.
【答案】(1)见解析; (2)见解析.
【解析】
(1)推导出AC⊥BC,AC⊥DC,从而AC⊥平面BCDE,由此能求出平面ADC⊥平面BCDE.
(2)分别存在点M和F,使得平面OMF∥平面ACD,取BC中点M,DE中点F,连结OM,MF,推导出OM∥AC,MF∥CD,由此推导出在线段DE和BC上存在中点M和F,平面OMF∥平面ACD.
证明:(1)∵△ABC的外接圆O的直径为AB,CD⊥平面ABC,BE∥CD,
∴AC⊥BC,AC⊥DC,
∵BC∩DC=C,
∴AC⊥平面BCDE,
∵AC平面ADC,∴平面ADC⊥平面BCDE.
(2)分别存在点M和F,使得平面OMF∥平面ACD,
取BC中点M,DE中点F,连结OM,MF,
∵O是AB的中点,∴OM∥AC,MF∥CD,
∵AC∩CD=C,OM∩MF=M,
AC、CD平面ACD,OM,MF平面OMF,
∴在线段DE和BC上存在中点M和F,平面OMF∥平面ACD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第
人参加“学雷锋”志愿活动,按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
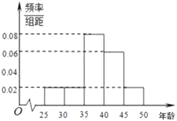
(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有
人参加社区宣传交流活动,求至少有![]() 人年龄在第
人年龄在第![]() 组的概率.
组的概率.