题目内容

9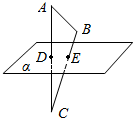．如图所示，D、E分别是△ABC的边AC、BC上的点，平面α经过D、E两点．
（1）求作直线AB与平面α的交点P；
（2）求证：D、E、P三点共线．

分析 （1）连结DE并延长，交AB延长线于点P，则点P为直线AB与平面α的交点．
（2）由已知得DE为平面α与平面ABC的交线，P∈AB，AB?平面ABC，且P∈α，由此能证明D、E、P三点共线．

解答 （1）解：连结DE并延长，交AB延长线于点P，则点P为直线AB与平面α的交点．
如右图．
（2）证明：∵D∈AC，E∈BC，
∴DE?平面ABC，
∵D∈α，E∈α，∴DE?α，
∵DE为平面α与平面ABC的交线，
又P∈AB，AB?平面ABC，且P∈α，
∴P在平面α与平面ABC的交线DE上，
∴D、E、P三点共线．

点评 本题考查直线与平面的交点的作法，考查三点共线的证明，是基础题，解题时要认真审题，注意平面的基本性质及推论的合理运用．

练习册系列答案
相关题目
19．函数f（x）=x2+lnx的零点个数为（　　）
A．0B．1C．2D．3
20．已知二次函数f（x）=x2-4x+1．
（1）当x∈[-2，1]时，求函数的最值；
（2）当x∈[-2，3]时，求函数的最值．
17．AB．AD?α，CB，CD?β，E∈AB．F∈BC，G∈CD，H∈DA，若直线EH与FG相交于点P，则P点必在直线BD上．
4．化简：
（1）$\frac{sinθ-cosθ}{tanθ-1}$．
（2）$\sqrt{si{n}^{2}θ-si{n}^{4}θ}$，θ是第二象限角．
14．在等比数列{an}中，
（1）若已知a2=4，a5=-$\frac{1}{2}$，求an；
（2）若已知a3a4a5=8，求a2a6的值．
1．已知函数f（x）是定义在R上的以2为周期的奇函数，当x∈[-1，1]时，f（x）=x2．
（1）当x∈[1，3]时，求f（x）的表达式；
（2）求f（-3），f（3.5）的值．
18．已知函数f（x）=|$\frac{1}{x}$-1|．
（1）求函数y=f（x）-3的零点；
（2）利用定义法判断函数f（x）在（0，1]上的单调性，并求出函数f（x）的单调区间；
（3）若存在实数a、b（a＜b且a≠0），使得集合{y|y=f（x），a≤x≤b}=[ma，mb]，求非零实数m的取值范围．
19．定义：若复数z与z1满足z•z1=1，则称复数z与z1互为倒数，已知复数z=i（2+3i），则复数z的倒数z1为（　　）
A．-$\frac{3}{13}+\frac{2}{13}$iB．-$\frac{3}{13}-\frac{2}{13}$iC．$\frac{3}{13}+\frac{2}{13}$iD．$\frac{3}{13}-\frac{2}{13}$i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网