题目内容

20．已知二次函数f（x）=x2-4x+1．
（1）当x∈[-2，1]时，求函数的最值；
（2）当x∈[-2，3]时，求函数的最值．

分析 分析函数的图象和性质，进而分析函数在给定区间上的单调性，可得答案．

解答 解：f（x）=x2-4x+1的图象是开口向上，对称轴为x=2的抛物线；
（1）由于抛物线的对称轴在区间[-2，1]的右侧，
因此函数在[-2，1]上单调递减，
所以，当x=-2时，函数取得最大值f（-2）=13，
当x=1时，函数取得最小值f（1）=-2
（2）由于对称轴在区间[-2，3]内，
所以，当x=2时，函数取得最小值f（2）=-3，
当x=-2时，函数取到最大值f（-2）=13．

点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．

练习册系列答案
相关题目
10．已知函数f（x）=ax2+b|x-1|，其中a，b∈（-4，4）且a≠0
（Ⅰ）当a∈（0，4），b=1时，求函数f（x）在[0，2]上的最小值；
（Ⅱ）若存在实数c，使函数g（x）=f（x）-c有四个不同的零点，求a+b的取值范围．
11．已知$f（x）=sin（\frac{π}{6}-2x）+1-2{cos^2}x$．
（Ⅰ）求函数f（x）的单调递减区间；
（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，且$a=1，b+c=2，f（A）=-\frac{1}{2}$，求△ABC的面积．
8．计算：
（1）log427×log58×log325
（2）（${a^{\frac{2}{3}}}{b^{\frac{1}{2}}}$）•（-3${a^{\frac{1}{2}}}{b^{\frac{1}{3}}}$）÷（$\frac{1}{3}{a^{\frac{1}{6}}}{b^{\frac{5}{6}}}$）
15．已知向量$\overrightarrow{a}$=（1，0），点A（4，4），点B为直线y=2x上一个动点．若$\overrightarrow{AB}$∥$\overrightarrow{a}$，则点B的坐标为（2，4）．
5．已知圆C：（x-3）2+（y-4）2=1和两点A（-m，0），B（m，0）（m＞0），若圆C上不存在点P，使得∠APB为直角，则实数m的取值范围是（0，4）∪（6，+∞）．
12．已知点P在线段AB上且$\overrightarrow{AP}=\overrightarrow{PB}$，若$\overrightarrow{AB}=λ\overrightarrow{PB}$，则λ=2．
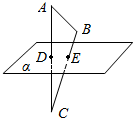9．如图所示，D、E分别是△ABC的边AC、BC上的点，平面α经过D、E两点．
（1）求作直线AB与平面α的交点P；
（2）求证：D、E、P三点共线．
10．已知sin（3π+α）=$\frac{1}{3}$，求：$\frac{sin（180°+α）cos（720°+α）tan（540°+α）•sin（-180°+α）}{tan（900°+α）•sin（-180°-α）•cos（-180°-α）}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网