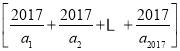题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,且直线
,且直线![]() 是曲线
是曲线![]() 的一条切线,求实数
的一条切线,求实数![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)代入a的值,根据切线方程得到关于x0的方程,求出切点坐标,解出m即可;
(2)问题转化为alnx![]() 1>0,记g(x)=alnx
1>0,记g(x)=alnx![]() 1,通过讨论a的范围,求出函数的单调区间,从而确定a的范围即可;
1,通过讨论a的范围,求出函数的单调区间,从而确定a的范围即可;
(3)法一:求出h(x2)﹣h(x1)的解析式,记m(x)=2[(x![]() )lnx
)lnx![]() x],x≥1,根据函数的单调性求出a的范围即可;
x],x≥1,根据函数的单调性求出a的范围即可;
法二:由h(x)=f(x)﹣x=alnx![]() x,x>0,以及h(x)有两个极值点x1,x2(x1<x2),得到x1+x2=a,x1x2=1,设t2
x,x>0,以及h(x)有两个极值点x1,x2(x1<x2),得到x1+x2=a,x1x2=1,设t2![]() (t>1),从而h(x2)﹣h(x1)
(t>1),从而h(x2)﹣h(x1)![]() 等价于 h(t)=(t
等价于 h(t)=(t![]() )lnt
)lnt![]() t
t![]() ,t>1,记m(x)=(x
,t>1,记m(x)=(x![]() )lnx
)lnx![]() x,x≥1,根据函数的单调性求出a的范围即可.
x,x≥1,根据函数的单调性求出a的范围即可.
(1)当![]() 时,
时,![]() ,
,![]() .
.
设直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,
,
则![]() ,即
,即![]() ,
,
解得![]() ,即切点为
,即切点为![]() ,
,
因为切点在![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
(2)不等式![]() 可化为
可化为![]() .
.
记![]() , 则
, 则![]() 对任意
对任意![]() 恒成立.
恒成立.
考察函数![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
所以![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,
,![]() ;
;![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 时,
时,![]() ,符合题意;
,符合题意;
若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.
(3)方法一:![]() ,
,![]() ,
,![]() .
.
因为![]() 有两个极值点
有两个极值点![]() ,
,![]() ,
,
所以![]() ,即
,即![]() 的两实数根为
的两实数根为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
从而![]()
![]()
![]()
![]() .
.
记![]() ,
,![]() .
.
则![]()
![]()
![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
不等式![]() 可化为
可化为![]() ,所以
,所以![]() .
.
因为![]() ,且
,且![]() 在
在![]() 上递增,所以
上递增,所以![]() ,
,
即![]() 的取值范围为
的取值范围为![]() .
.
方法二:![]() ,
,![]() ,
,![]() .
.
因为![]() 有两个极值点
有两个极值点![]() ,
,![]() ,
,
所以![]() ,即
,即![]() 的两实数根为
的两实数根为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
从而![]() 等价于
等价于![]() ,
,![]() .
.
记![]() ,
,![]() .
.
则![]()
![]() (当且仅当
(当且仅当![]() 时取等号),
时取等号),
所以![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() ,且
,且![]() 在
在![]() 上递增,所以
上递增,所以![]() ,
,
即![]() 的取值范围为
的取值范围为![]() .
.