题目内容
二次函数f(x)=px2+qx+r中实数p、q、r满足 =0,其中m>0,求证:
=0,其中m>0,求证:
(1)pf( )<0;
)<0;
(2)方程f(x)=0在(0,1)内恒有解.
 =0,其中m>0,求证:
=0,其中m>0,求证:(1)pf(
 )<0;
)<0;(2)方程f(x)=0在(0,1)内恒有解.
证明略
(1)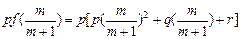
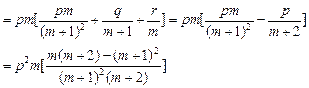
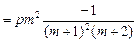 ,由于f(x)是二次函数,故p≠0,又m>0,所以,pf(
,由于f(x)是二次函数,故p≠0,又m>0,所以,pf( )<0.
)<0.
(2)由题意,得f(0)=r,f(1)=p+q+r
①当p<0时,由(1)知f( )<0
)<0
若r>0,则f(0)>0,又f( )<0,所以f(x)=0在(0,
)<0,所以f(x)=0在(0, )内有解;
)内有解;
若r≤0,则f(1)=p+q+r=p+(m+1)=(-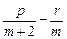 )+r=
)+r=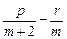 >0,
>0,
又f( )<0,所以f(x)=0在(
)<0,所以f(x)=0在( ,1)内有解.
,1)内有解.
②当p<0时同理可证.
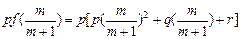
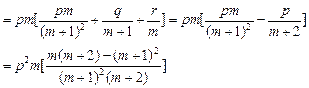
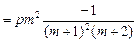 ,由于f(x)是二次函数,故p≠0,又m>0,所以,pf(
,由于f(x)是二次函数,故p≠0,又m>0,所以,pf( )<0.
)<0.(2)由题意,得f(0)=r,f(1)=p+q+r
①当p<0时,由(1)知f(
 )<0
)<0若r>0,则f(0)>0,又f(
 )<0,所以f(x)=0在(0,
)<0,所以f(x)=0在(0, )内有解;
)内有解;若r≤0,则f(1)=p+q+r=p+(m+1)=(-
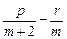 )+r=
)+r=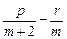 >0,
>0,又f(
 )<0,所以f(x)=0在(
)<0,所以f(x)=0在( ,1)内有解.
,1)内有解.②当p<0时同理可证.

练习册系列答案
相关题目
 km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省?
km处的海岸渔站中,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸可以使抵达渔站的时间最省? 型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润
型电脑.1993年这种电脑每台平均生产成本为5000元,并以纯利润 确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管
确定出厂价.从1994年开始,公司通过更新设备和加强管理,使生产成本逐年降低.到1997年,尽管 ,但却实现了
,但却实现了 纯利润的高效益.
纯利润的高效益. ,以下数据可供参考:
,以下数据可供参考: ,
, ).
). ,f2(x)=x+2,
,f2(x)=x+2, ,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;
,试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积; ],求b的值.
],求b的值. 




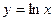 在点
在点 处的切线的斜率是_________,切线的方程为_______________;
处的切线的斜率是_________,切线的方程为_______________;