题目内容
已知二次函数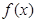 满足条件
满足条件 ,及
,及 .
.
(1)求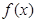 的解析式;
的解析式;
(2)求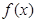 在
在 上的最值.
上的最值.
(1)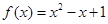 ;(2)
;(2) .
.
解析试题分析:
解题思路:(1)设出二次函数解析式,代入 ,及
,及 ,求系数
,求系数 即可;(2)利用配方法得出二次函数的对称轴,进而研究函数在
即可;(2)利用配方法得出二次函数的对称轴,进而研究函数在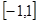 上的单调性,再求最值.
上的单调性,再求最值.
规律总结:(1)已知函数类型求函数的解析式,要利用待定系数法;(2)求二次函数的最值时,往往利用配方法得出对称轴、单调区间,再利用图像研究最值.
试题解析:设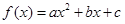 ,
,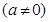
则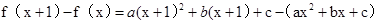
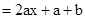
∴由题 c="1" ,2ax+a+b=2x 恒成立
∴ 2a="2" ,a+b=0, c=1 得 a="1" b="-1" c=1 ∴
(2) 在
在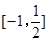 单调递减,在
单调递减,在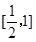 单调递增
单调递增
∴f(x)min=f( )=
)= ,f(x)max=f(-1)=3.
,f(x)max=f(-1)=3.
考点:1.待定系数法;2.一元二次函数的最值.

练习册系列答案
相关题目
 ,
, ,
, .
. 时,求函数
时,求函数 的最小值;
的最小值; ,令
,令 ,求
,求 的取值范围.
的取值范围.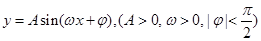 的最小值是
的最小值是 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是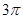 ,又:图象过点
,又:图象过点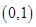 ,
, 的集合;
的集合; 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时,有
时,有

 对
对 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 满足下列关系:
满足下列关系:
 (
( 为非零常数)
为非零常数)

 的解析式为
的解析式为 .
.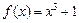 的反函数
的反函数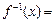 .
.