题目内容
【题目】选修4-4:极坐标与参数方程
在极坐标系中,已直曲线![]() ,将曲线C上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C1,又已知直线
,将曲线C上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C1,又已知直线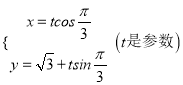 ,且直线
,且直线![]() 与C1交于A、B两点,
与C1交于A、B两点,
(1)求曲线C1的直角坐标方程,并说明它是什么曲线;
(2)设定点![]() , 求
, 求![]() 的值;
的值;
【答案】(1)![]() 曲线
曲线![]() 是焦点
是焦点![]() ,长轴长为4的椭圆(2)
,长轴长为4的椭圆(2)![]()
【解析】试题分析:(1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,化曲线C1的方程为(x﹣1)2+y2=1,再由图象的伸缩变换可得曲线C1;
(2)将直线l的参数方程代入曲线C的方程![]() 中,得到关于t的二次方程,运用韦达定理,参数的几何意义,即可求
中,得到关于t的二次方程,运用韦达定理,参数的几何意义,即可求![]() .
.
试题解析:
(1)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,即
,即![]() ∴曲线
∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ∴曲线
∴曲线![]() 是焦点
是焦点![]() ,
,![]() 长轴长为4的椭圆.
长轴长为4的椭圆.
解(2)将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的方程
的方程![]() 中得
中得![]() ,
,
设![]() 对应的参数为
对应的参数为![]() 、
、![]() ∴
∴![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
∴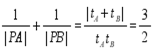 .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
【题目】某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如表:
停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为![]() 小时,求
小时,求![]() 的值;
的值;
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠![]() 小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.