题目内容

【题目】已知圆C与两平行直线 x﹣y﹣8=0和x﹣y+4=0相切，圆心在直线2x+y﹣10=0上．
（1）求圆C的方程．
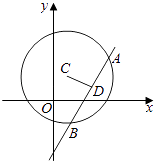
（2）过原点O做一条直线，交圆C于M，N两点，求OM*ON的值．

【答案】
（1）解：设所求圆的方程是（x﹣a）2+（y﹣b）2=r2．

由题意知，两平行线间距离d= =6 ，

又到两平行直线距离相等的直线方程为：x﹣y﹣2=0

所以由 ，得 ．即圆心坐标为（4，2）．

所以圆C的方程为：（x﹣4）2+（y﹣2）2=18\


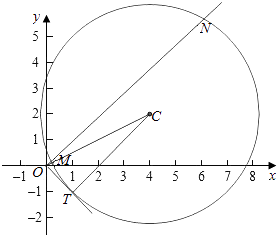
（2）解：设OT是圆的切线，切点为T，

则OT= = = ，

则由切割线定理可得：OM*ON=OT2=2


【解析】（1）利用待定系数法进行求解即可．（2）根据切割线定理，求出切线长即可．

练习册系列答案
相关题目

【题目】已知函数y=ax（a＞0且a≠1）在区间[1，2]上的最大值与最小值之和为12，则实数a的值为（ ）
A.
B.2
C.3
D.4

【题目】已知函数的图象与轴相切，且切点在轴的正半轴上.

（1）若函数在上的极小值不大于，求的取值范围；

（2）设（），证明： 在上的最小值为定值.

【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之，问各出几何？此问题的译文是:今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还，他们各应偿还多少？已知牛、马、羊的主人各应偿还升， 升， 升，1斗为10升，则下列判断正确的是( )

A. ， ， 依次成公比为2的等比数列，且

B. ， ， 依次成公比为2的等比数列，且

C. ， ， 依次成公比为的等比数列，且

D. ， ， 依次成公比为的等比数列，且

【题目】如图，已知正方形ABCD的中心为E（﹣1，0），一边AB所在的直线方程为x+3y﹣5=0，求其它三边所在的直线方程．

【题目】为调查长沙市中学生平均每人每天参加体育锻炼时间（单位：分钟），按锻炼时间分下一列四种情况统计：①0～10分钟；②11～20分钟；③21～30分钟；④30分钟以上．有l0 000名中学生参加了此项活动，如图是此次调查中某一项的流程图，其输出的结果是6 200，则平均每天参加体育锻炼时间在0～20分钟内的学生的频率是 ．

【题目】从某学校高三年级共800名男生中随机抽取50名测量身高，测量发现被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160）、第二组[160，165）；…第八组[190，195]，右图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．

（1）估计这所学校高三年级全体男生身高180cm以上（含180cm）的人数；
（2）求第六组、第七组的频率并补充完整频率分布直方图；
（3）若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记他们的身高分别为x、y，求满足|x﹣y|≤5的事件概率．

【题目】已知圆C：（x﹣1）2+（y﹣2）2=25，直线l：（2m+1）x+（m+1）y﹣7m﹣4=0（m∈R）．

（1）求证：无论m取什么实数，直线l恒过第一象限；
（2）求直线l被圆C截得的弦长最短时m的值以及最短长度；
（3）设直线l与圆C相交于A、B两点，求AB中点M的轨迹方程．

【题目】已知圆心为（1，1）的圆C经过点M（1，2）．
（1）求圆C的方程；
（2）若直线x+y+m=0与圆C交于A、B两点，且△ABC是直角三角形，求实数m．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网