题目内容
11.已知A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(0,1)、F(2,1)、G(4,2)七个点,抛物线y=a(x-1)2+k(a≠0)经过其中的三个点.(1)当a<0时,求a和k的值;
(2)判定C、G两点是否能同时在抛物线y=a(x-1)2+k(a≠0)上,若能,求出a和k的值;若不能,请说明理由;
(3)若抛物线经过七个点中的三个,直接写出所有满足这样的条件的抛物线条数.
分析 (1)由抛物线开口向下,可得经过A,B,D,代入方程,即可得到a,k;
(2)假设C、G两点同时在抛物线y=a(x-1)2+k(a≠0)上,代入C,G的坐标,解方程可得a=0,即可判断是否存在;
(3)运用二次函数的对称性,结合图形即可得到所求抛物线的条数.
解答 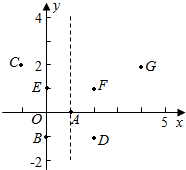 解:(1)当a<0,抛物线开口向下,
解:(1)当a<0,抛物线开口向下,
若顶点为A,则k=0,经过B,D两点,
即有-1=a(0-1)2,解得a=-1;
若顶点不为A,若经过B,则经过D,必过A,矛盾;
若经过E,则过F,由x=1的左边图象上升,右边下降,
则不存在经过第三个点.
故a=-1,k=0成立;
(2)假设C、G两点同时在抛物线y=a(x-1)2+k(a≠0)上,
即有2=a(-1-1)2+k,2=a(4-2)2+k,
解得a=0,与a≠0矛盾,
故不能同时在抛物线y=a(x-1)2+k(a≠0)上;
(3)由于对称轴为x=1,
若抛物线开口向下,则经过A,B,D三点,
若抛物线开口向上,则经过A,E,F三点.
故满足这样的条件的抛物线条数为2.
点评 本题考查抛物线方程的求法,考查二次函数的对称性的运用,数形结合是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
9.将两枚质地均匀的骰子各掷一次,设事件A为两个点数都不相同,设事件B为两个点数和是7或8,则P(B|A)=( )
| A. | $\frac{1}{3}$ | B. | $\frac{5}{18}$ | C. | $\frac{10}{11}$ | D. | $\frac{1}{2}$ |
2.已知两向量$\overrightarrow{a}$=(cos23°,cos67°),$\overrightarrow{b}$=(2cos68°,2cos22°),则$\overrightarrow{a}$$•\overrightarrow{b}$=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |