题目内容
9.若$\underset{lim}{n→∞}$($\frac{{n}^{3}-1}{{n}^{2}-3n+1}$+an+b)=1,则a+b=-3.分析 $\frac{{n}^{3}-1}{{n}^{2}-3n+1}$+an+b=(1+a)n+(3+b)+$\frac{8n-4}{{n}^{2}-3n+1}$,$\underset{lim}{n→∞}$($\frac{{n}^{3}-1}{{n}^{2}-3n+1}$+an+b)=1,可得1+a=0,3+b=1,解出即可.
解答 解:∵$\frac{{n}^{3}-1}{{n}^{2}-3n+1}$+an+b=(1+a)n+(3+b)+$\frac{8n-4}{{n}^{2}-3n+1}$,$\underset{lim}{n→∞}$($\frac{{n}^{3}-1}{{n}^{2}-3n+1}$+an+b)=1,
∴1+a=0,3+b=1,
∴a+b=-3.
故答案为:-3.
点评 本题考查了代数式的化简、极限的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
19.下列方程中,以x±2y=0为渐近线的双曲线是( )
| A. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1 |
14.不共面的四点可以确定不同的线段数为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
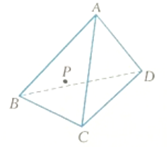 如图,一个四面体木块ABCD,在△ABC的面内有一点P,要经过点P在平面ABC内画一条直线l,使l⊥AD,怎样画?写出作法,并给予证明.
如图,一个四面体木块ABCD,在△ABC的面内有一点P,要经过点P在平面ABC内画一条直线l,使l⊥AD,怎样画?写出作法,并给予证明.