题目内容
（2013•天津）设a+b=2，b＞0，则当a= _________ 时，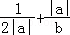
取得最小值．
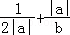取得最小值．﹣2
∵a+b=2，b＞0，
∴
=
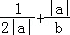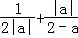，（a＜2）
设f（a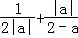）=，（a＜2），画出此函数的图象，如图所示．
利用导数研究其单调性得，
当a＜0时，f（a）=﹣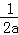
+
，
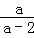f′（a）=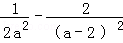
=
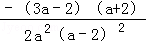，当a＜﹣2时，f′（a）＜0，当﹣2＜a＜0时，f′（a）＞0，
故函数在（﹣∞，﹣2）上是减函数，在（﹣2，0）上是增函数，
∴当a=﹣2时，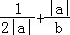
取得最小值
．
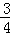同样地，当0＜a＜2时，得到当a=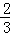
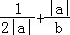时，取得最小值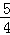
．
综合，则当a=﹣2时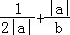，取得最小值．
故答案为：﹣2．
∴
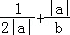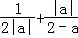=，（a＜2）设f（a）=
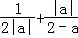，（a＜2），画出此函数的图象，如图所示．利用导数研究其单调性得，
当a＜0时，f（a）=﹣
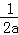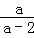+，f′（a）=
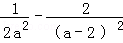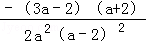=，当a＜﹣2时，f′（a）＜0，当﹣2＜a＜0时，f′（a）＞0，故函数在（﹣∞，﹣2）上是减函数，在（﹣2，0）上是增函数，
∴当a=﹣2时，
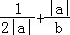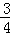取得最小值．同样地，当0＜a＜2时，得到当a=
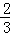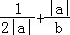时，取得最小值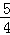．综合，则当a=﹣2时，
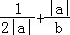取得最小值．故答案为：﹣2．
练习册系列答案
相关题目
的函数
同时满足以下三个条件：
，总有
；（2）
；（3） 若
，
，且
，则有
成立，则称
的值； 
在区间
，使得
且
， 求证：
.
log2x，则f(2)＝________.
＋2的图象关于点A(0,1)对称．
]=[x]
在
内 （ ）
km．D为海湾一侧海岸线CT上的一点，设CD＝x(km)，点D对跑道AB的视角为q．
，若f(－4)＝f(0)，f(－2)＝0，则关于x的不等式f(x)≤1的解集为( )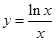
的最大值为( )
