题目内容
设 :函数
:函数 在
在 内单调递减;
内单调递减; :曲线
:曲线 与
与 轴交于不同的两点.
轴交于不同的两点.
(1)若 为真且
为真且 为真,求
为真,求 的取值范围;
的取值范围;
(2)若 与
与 中一个为真一个为假,求
中一个为真一个为假,求 的取值范围.
的取值范围.
 :函数
:函数 在
在 内单调递减;
内单调递减; :曲线
:曲线 与
与 轴交于不同的两点.
轴交于不同的两点.(1)若
 为真且
为真且 为真,求
为真,求 的取值范围;
的取值范围;(2)若
 与
与 中一个为真一个为假,求
中一个为真一个为假,求 的取值范围.
的取值范围.(1)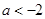 ,(2)
,(2)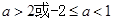
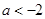 ,(2)
,(2)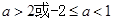
试题分析:(1)因为若
 :函数
:函数 在
在 内单调递减为真;而一次函数增减性决定于一次项系数的正负,所以
内单调递减为真;而一次函数增减性决定于一次项系数的正负,所以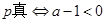 ,因为
,因为 :曲线
:曲线 与
与 轴交于不同的两点为真,即方程
轴交于不同的两点为真,即方程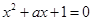 有两个不同的交点,因此
有两个不同的交点,因此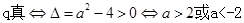 ,因此若
,因此若 为真且
为真且 为真,则
为真,则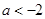 ,(2)若
,(2)若 与
与 中一个为真一个为假,则有
中一个为真一个为假,则有 为真
为真 为假
为假 或
或 为真
为真 为假
为假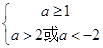 ,即
,即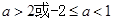
由题意得,因为若
 :函数
:函数 在
在 内单调递减为真;而一次函数增减性决定于一次项系数的正负,所以
内单调递减为真;而一次函数增减性决定于一次项系数的正负,所以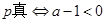 ,因为
,因为 :曲线
:曲线 与
与 轴交于不同的两点为真,即方程
轴交于不同的两点为真,即方程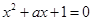 有两个不同的交点,因此
有两个不同的交点,因此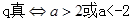 -4分
-4分(1)若
 为真且
为真且 为真,则
为真,则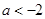 -7分
-7分(2)若
 与
与 中一个为真一个为假,则有
中一个为真一个为假,则有 为真
为真 为假
为假 或
或 为真
为真 为假
为假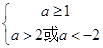 ,即
,即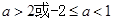 -14分
-14分
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
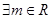 ,使
,使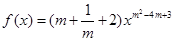 是幂函数;
是幂函数; 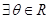 ,使
,使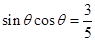 成立;
成立;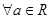 ,使
,使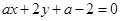 恒过定点;
恒过定点; ,不等式
,不等式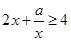 成立的充要条件
成立的充要条件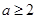 .
.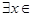 R使得
R使得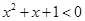 ”的否定是:“
”的否定是:“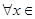 R均有
R均有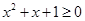 ”;
”;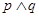 为假命题,则p,q均为假命题;
为假命题,则p,q均为假命题;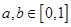 ,则不等式
,则不等式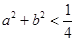 成立的概率是
成立的概率是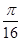 ;
;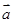 与
与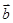 的夹角是钝角”的必要不充分条件是“
的夹角是钝角”的必要不充分条件是“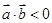 ”.
”.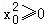
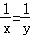 ,则x=y
,则x=y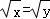
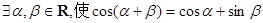 ;
;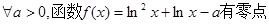
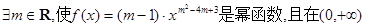 上递减
上递减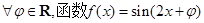 都不是偶函数
都不是偶函数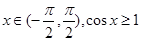 ;命题q:任意
;命题q:任意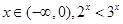 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )

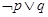

 x∈R,x+
x∈R,x+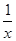 =2;
=2; x∈R,x2>0;
x∈R,x2>0;