题目内容
(本小题满分14分)
袋中装有黑球和白球共7个,从中任取1个球是白球的概率为 .现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
(1)求取球2次终止的概率;
(2)求甲取到白球的概率.
袋中装有黑球和白球共7个,从中任取1个球是白球的概率为
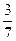 .现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.(1)求取球2次终止的概率;
(2)求甲取到白球的概率.
(1)
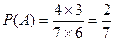
(2)
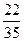
解:(1)设袋中原有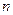 个白球,由题意得
个白球,由题意得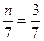 .∴
.∴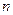 ="3. "
="3. "
即袋中原有3个白球. ………( 4分)
记“取球两次终止”的事件为A,则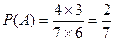 .………(8分)
.………(8分)
(2)因为甲先取,所以甲只有在第1次,第3次,第5次取球,
记“甲取到白球”的事件为B,“第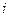 次取出的球是白球”为
次取出的球是白球”为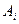 ,(i=1,2,…5)
,(i=1,2,…5)
则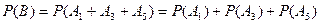
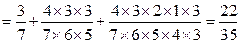 ……………(14分)
……………(14分)
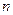 个白球,由题意得
个白球,由题意得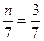 .∴
.∴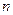 ="3. "
="3. " 即袋中原有3个白球. ………( 4分)
记“取球两次终止”的事件为A,则
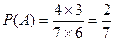 .………(8分)
.………(8分)(2)因为甲先取,所以甲只有在第1次,第3次,第5次取球,
记“甲取到白球”的事件为B,“第
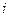 次取出的球是白球”为
次取出的球是白球”为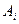 ,(i=1,2,…5)
,(i=1,2,…5)则
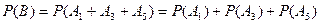
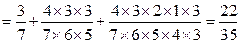 ……………(14分)
……………(14分)
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 2分)
2分)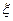 ,求随机变量
,求随机变量 .
.



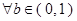 ,则方程
,则方程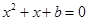 有实根的概率为 ( )
有实根的概率为 ( )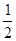
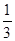
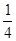

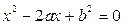 的系数a在[0,2]内取值,b在[0,3]内取值,求使方程没有实根的概率.
的系数a在[0,2]内取值,b在[0,3]内取值,求使方程没有实根的概率. :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率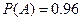 .
.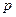 ;
;
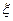 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求 若甲破译的成功率为
若甲破译的成功率为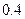 ,乙破译的成功率为
,乙破译的成功率为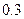 ,则密码破译成功的概率等于
,则密码破译成功的概率等于 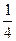 ,则此长方体的体积是 .
,则此长方体的体积是 .