题目内容
已知数列{an}满足: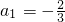 ,
,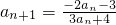 (n∈N+).
(n∈N+).
(1)证明数列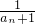 是等差数列,并求{an}的通项公式;
是等差数列,并求{an}的通项公式;
(2)数列{bn}满足: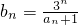 (n∈N+),求{bn}的前n项和Sn.
(n∈N+),求{bn}的前n项和Sn.
(1)证明:因为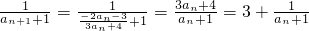
所以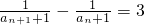
所以{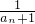 }是首项为3,公差为3的等差数列,
}是首项为3,公差为3的等差数列,
所以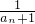 =3n,
=3n,
所以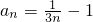 ;
;
(2)解:由已知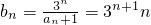
∴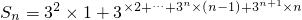 ①
①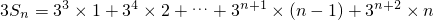 ②
②
①-②得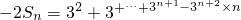 =
=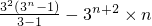
所以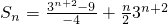 =
= .
.
分析:(1)由数列递推式两边加上1,再取倒数,即可证得数列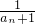 是等差数列,从而可求{an}的通项公式;
是等差数列,从而可求{an}的通项公式;
(2)确定数列的通项.利用错位相减法,即可求{bn}的前n项和Sn.
点评:本题考查等差数列的证明,考查数列的通项与求和,考查学生的计算能力,属于中档题.
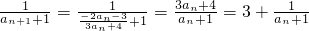
所以
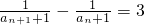
所以{
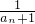 }是首项为3,公差为3的等差数列,
}是首项为3,公差为3的等差数列,所以
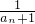 =3n,
=3n,所以
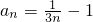 ;
;(2)解:由已知
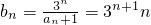
∴
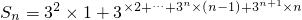 ①
①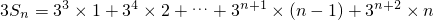 ②
②①-②得
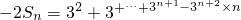 =
=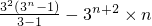
所以
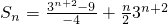 =
= .
.分析:(1)由数列递推式两边加上1,再取倒数,即可证得数列
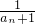 是等差数列,从而可求{an}的通项公式;
是等差数列,从而可求{an}的通项公式;(2)确定数列的通项.利用错位相减法,即可求{bn}的前n项和Sn.
点评:本题考查等差数列的证明,考查数列的通项与求和,考查学生的计算能力,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目