题目内容
18．设两个非零向量$\overrightarrow{a}$与$\overrightarrow{b}$不共线，若$\overrightarrow{AB}$=$\overrightarrow{a}+\overrightarrow{b}$，$\overrightarrow{BC}$=$\overrightarrow{a}+10\overrightarrow{b}$，$\overrightarrow{CD}$=3（$\overrightarrow{a}-2\overrightarrow{b}$），则（ ）| A． | A，B，C三点共线 | B． | B，C，D三点共线 | C． | A，C，D三点共线 | D． | A，B，D三点共线 |
分析 利于已知条件表示$\overrightarrow{BD}$，判断与$\overrightarrow{AB}$共线，推出结果．
解答 解：两个非零向量$\overrightarrow{a}$与$\overrightarrow{b}$不共线，若$\overrightarrow{AB}$=$\overrightarrow{a}+\overrightarrow{b}$，$\overrightarrow{BC}$=$\overrightarrow{a}+10\overrightarrow{b}$，$\overrightarrow{CD}$=3（$\overrightarrow{a}-2\overrightarrow{b}$），
所以$\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{a}+10\overrightarrow{b}+3（\overrightarrow{a}-2\overrightarrow{b}）$=$4（\overrightarrow{a}+\overrightarrow{b}）$=4$\overrightarrow{AB}$，
所以$\overrightarrow{AB}\stackrel{\;}{，}\overrightarrow{BD}$共线，又因为它们有公共点B，所以A、B、D共线．
故选：D．
点评 本题考查向量共线的充要条件的应用，考查计算能力．
练习册系列答案
相关题目
9．已知复数z满足|z|+z=1+3i（i为虚数单位），则复数z在复平面所对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
6．如图所示的程序框图，其运行结果（即输出的S值）是（ ）
| A． | 5 | B． | 20 | C． | 30 | D． | 42 |
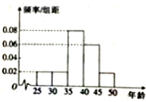2015年某企业员工有500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．现在要从年龄较小的第1，3，4组中用分层抽样的方法抽取16人，则在第4组抽取的人数为（ ）