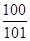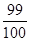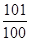题目内容
等差数列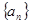 中,
中,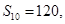 那么
那么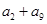 的值是( )
的值是( )
| A.12 | B.24 | C.16 | D.48 |
B
解析试题分析:根据Sn= 因为n=10,
因为n=10,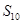 =120
=120
所以120= ,所以
,所以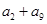 =24,故选B。
=24,故选B。
考点:本题主要考查等差数列的性质及求和公式。
点评:基础题,灵活运用等差数列的性质,能简化解题过程。

练习册系列答案
相关题目
已知数列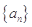 满足
满足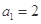 ,
,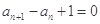
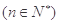 ,则此数列的通项
,则此数列的通项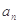 等于( )
等于( )
A.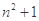 | B.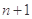 | C.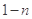 | D.3-n |
等差数列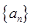 中,如果
中,如果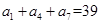 ,
,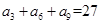 ,数列
,数列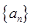 前9项的和为( )
前9项的和为( )
| A.297 | B.144 | C.99 | D.66 |
如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.若2013是第m行从左至右算的第n个数字,则(m,n)为( )
| A.(63,60) | B.(63,4) | C.(64,61) | D.(64,4) |
等差数列{an}的前n项和为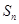 .已知
.已知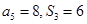 ,则
,则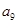 = ( )
= ( )
| A.8 | B.12 | C.16 | D.24 |
已知-1,a,b,-4成等差数列,-1,c,d, e,-4成等比数列,则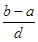 =( )
=( )
A.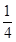 | B.-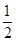 | C.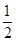 | D.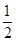 或- 或-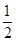 |
在等差数列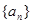 中,
中,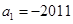 ,前n项和为
,前n项和为 ,且
,且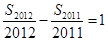 ,则
,则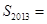
A.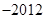 | B.2012 | C.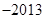 | D.2013 |
已知等差数列 与等比数列
与等比数列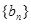 各项都是正数,且
各项都是正数,且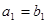 ,
, ,那么一定有( )
,那么一定有( )
A. | B.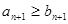 | C. | D. |
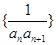 的前100项和为( )
的前100项和为( )