题目内容
已知-1,a,b,-4成等差数列,-1,c,d, e,-4成等比数列,则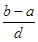 =( )
=( )
A.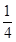 | B.-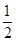 | C.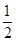 | D.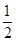 或- 或-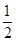 |
C
解析试题分析:因为-1,a,b,-4成等差数列,所以公差为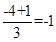 ,所以
,所以 ;因为-1,c,d, e,-4成等比数列,所以
;因为-1,c,d, e,-4成等比数列,所以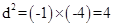 ,
, ,所以
,所以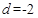 。所以
。所以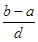 =
=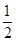 。
。
考点:等差数列的性质;等比数列的性质。
点评:在等比数列中,所有的奇数项一定同号,所有的偶数项也一定同号。

练习册系列答案
相关题目
设数列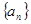 是等差数列,且
是等差数列,且 ,则这个数列的前5项和
,则这个数列的前5项和 =( )
=( )
| A. 10 | B. 15 | C. 20 | D. 25 |
实数 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
等差数列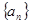 中,
中,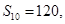 那么
那么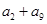 的值是( )
的值是( )
| A.12 | B.24 | C.16 | D.48 |
已知 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命
题,假命题的是( )
A.公差 ; ; | B.在所有 中, 中, 最大; 最大; |
C.满足 的 的 的个数有11个; 的个数有11个; | D. ; ; |
等差数列{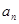 }的前n项和为
}的前n项和为 ,则常数
,则常数 = ( )
= ( )
| A.-2 | B.2 | C.0 | D.不确定 |
已知 表示等差数列
表示等差数列 的前
的前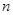 项和,且
项和,且 等于( )
等于( )
A. | B. | C. | D. |
等差数列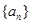 中,
中, ,则
,则 的值是( )
的值是( )
| A.12 | B.24 | C.36 | D.48 |
已知等差数列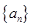 的通项公式
的通项公式 ,则
,则 等于 ( )
等于 ( )
| A.1 | B.2 | C.0 | D.9 |