题目内容
如图是从事网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推.若2013是第m行从左至右算的第n个数字,则(m,n)为( )
| A.(63,60) | B.(63,4) | C.(64,61) | D.(64,4) |
B
解析试题分析:根据题意可知,每一行的数的个数成等差数列,所以前62行共有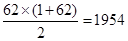 ,所以低63行第一个数为1955,从右向左数,所以2013是从由左向右数第4个数.
,所以低63行第一个数为1955,从右向左数,所以2013是从由左向右数第4个数.
考点:本小题主要考查等差数列的求和.
点评:解决本小题的关键是求出前62行的个数,再看出第63行是从由向左数的.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知等差数列 满足,
满足, ,则前n项和
,则前n项和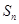 取最大值时,n的值为
取最大值时,n的值为
| A.20 | B.21 | C.22 | D.23 |
等差数列 的前n项和为
的前n项和为 ,且9
,且9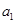 ,3
,3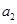 ,
,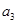 成等比数列. 若
成等比数列. 若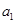 =3,则
=3,则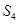 = ( )
= ( )
| A.7 | B.8 | C.12 | D. 16 |
实数 成等差数列,
成等差数列, 成等比数列,则
成等比数列,则 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
数列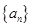 的首项为
的首项为 ,
,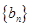 为等差数列且
为等差数列且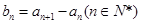 .若则
.若则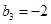 ,
,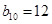 ,则
,则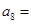 ( )
( )
| A.0 | B.3 | C.8 | D.11 |
等差数列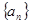 中,
中,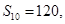 那么
那么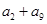 的值是( )
的值是( )
| A.12 | B.24 | C.16 | D.48 |
已知 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命
题,假命题的是( )
A.公差 ; ; | B.在所有 中, 中, 最大; 最大; |
C.满足 的 的 的个数有11个; 的个数有11个; | D. ; ; |
已知 表示等差数列
表示等差数列 的前
的前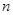 项和,且
项和,且 等于( )
等于( )
A. | B. | C. | D. |
设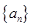 是等差数列,且
是等差数列,且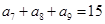 ,则其前15项和
,则其前15项和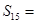 ( )
( )
| A.15 | B.45 | C.75 | D.105 |