题目内容
已知数列{ }的前
}的前 项和为
项和为


(1)求证:数列 是等比数列;
是等比数列;
(2)设数列{ }的前
}的前 项和为
项和为 ,求
,求 。
。
 }的前
}的前 项和为
项和为


(1)求证:数列
 是等比数列;
是等比数列;(2)设数列{
 }的前
}的前 项和为
项和为 ,求
,求 。
。(1)证明: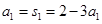 得
得
当 ≥2时,根据
≥2时,根据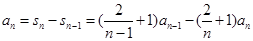 ,
,
整理得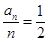 ×
×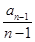 (
( ≥2),证得数列{
≥2),证得数列{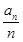 }是首项及公比均为
}是首项及公比均为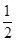 的等比数列。
的等比数列。
(2)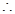
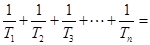
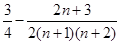
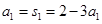 得
得
当
 ≥2时,根据
≥2时,根据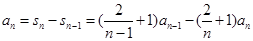 ,
,整理得
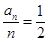 ×
×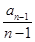 (
( ≥2),证得数列{
≥2),证得数列{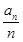 }是首项及公比均为
}是首项及公比均为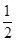 的等比数列。
的等比数列。(2)
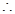
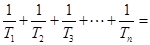
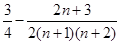
试题分析:(1)证明:
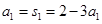 得
得
当
 ≥2时,由
≥2时,由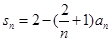 得
得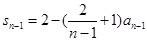 ,
,于是
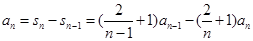 ,
,整理得
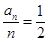 ×
×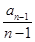 (
( ≥2),
≥2),所以数列{
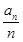 }是首项及公比均为
}是首项及公比均为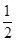 的等比数列。 6分
的等比数列。 6分(2)由(1)得
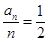 ×
×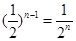 。
。于是
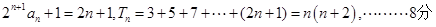 ,
,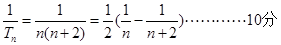
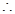
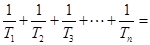
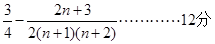
点评:中档题,本题具有较强的综合性,本解答从确定通项公式入手,认识到数列的特征,利用“裂项相消法”达到求和目的。“分组求和法”“裂项相消法”“错位相减法”是高考常常考到数列求和方法。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
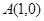 ,
, 、
、 、
、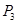 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且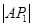 、
、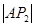 、
、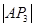 成等差数列,公差为
成等差数列,公差为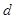 ,
,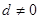 .
.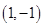 ,
,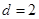 ,点
,点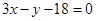 上时,求点
上时,求点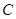 的方程是
的方程是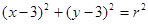
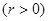 ,过点
,过点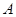 的直线交圆于
的直线交圆于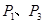 两点,
两点,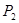 是圆
是圆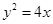 上,点
上,点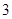 ,求证:线段
,求证:线段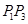 的垂直平分线与
的垂直平分线与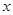 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标.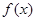 对任意
对任意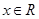 都有
都有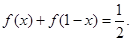
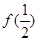 和
和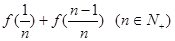 的值.
的值.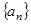 满足:
满足: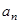 =
=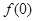 +
+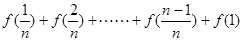 ,数列
,数列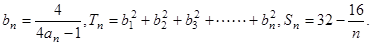 试比较
试比较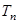 与
与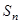 的大小.
的大小.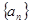 ,
,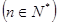 是等差数列,则数列
是等差数列,则数列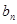 =
=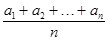
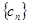 是等比数列,且
是等比数列,且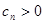 ,
, 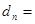 ____________
____________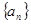 的公差为2,若
的公差为2,若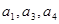 成等比数列, 则
成等比数列, 则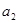 =( )
=( )



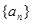 是单调递增的等差数列,首项
是单调递增的等差数列,首项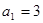 ,前
,前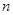 项和为
项和为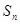 ,数列
,数列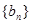 是等比数列,首项
是等比数列,首项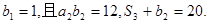
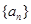 和
和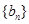 的通项公式.
的通项公式.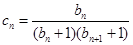 ,数列
,数列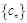 的前
的前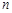 项和为
项和为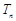 ,求证:
,求证: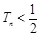 .
.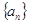 的首项为1,其前n项和为
的首项为1,其前n项和为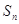 ,
,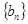 是公比为正整数的等比数列,其首项为3,前n项和为
是公比为正整数的等比数列,其首项为3,前n项和为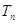 . 若
. 若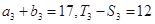 .
.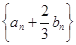 的前n项和
的前n项和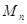 .(5分)
.(5分) .
. (
( ),其中
),其中 表示第
表示第 个月的兔子的总对数,
个月的兔子的总对数, ,则
,则 的值为( )
的值为( )