题目内容
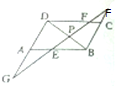
10. 在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90°,AB=1,AD=2,ABEF为正方形,平面ABEF⊥平面ABCD,P为DF的中点.AN⊥CF,垂足为N.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90°,AB=1,AD=2,ABEF为正方形,平面ABEF⊥平面ABCD,P为DF的中点.AN⊥CF,垂足为N.(1)求证:BF∥平面PAC;
(2)求证:AN⊥平面CDF;
(3)求三棱锥B-CEF的体积.
分析 (1)把证线面平行转化为证线线平行,连接BD交AC于O,连接PO,由三角形的中位线定理证得答案;
(2)证明AN⊥平面CDF,可证AN垂直于平面CDF内二相交直线,先由面面垂直的性质证明AF⊥CD,进一步证明CD⊥平面ACF,得到CD⊥AN,再由AN⊥CF得答案;
(3)把三棱锥B-CEF的体积转化为C-BEF的体积求解.
解答  (1)证明:如图,
(1)证明:如图,
连接BD交AC于O,连接PO,
∵PO为△BDF的中位线,∴PO∥EF,
∵PO?平面ACP,BF?平面ACP,
∴BF∥平面ACP;
(2)证明:∵平面ABEF⊥平面ABCD,交线为AB,
AF⊥AB,
∴AF⊥平面ABCD,
∵CD?平面ABCD,
∴AF⊥CD,
又∵CD⊥AC,AC∩AF=A,且AC,AF?平面ACF,
∴CD⊥平面ACF,则CD⊥AN,
∵AN⊥CF,且CD,CF为平面CDF内二相交直线,
∴AN⊥平面CDF;
(3)解:∵平面ABEF⊥平面ABCD,交线为AB,
又CA⊥AB,
∴CA⊥平面ABEF,
则CA=$\sqrt{B{C}^{2}-B{A}^{2}}=\sqrt{3}$,
∴${V}_{B-CEF}={V}_{C-BEF}=\frac{1}{3}{S}_{△BEF}•CA$=$\frac{1}{3}•\frac{1}{2}•1•1•\sqrt{3}=\frac{\sqrt{3}}{6}$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
相关题目
5. 重庆巴蜀中学高三的某位学生的10次数学考试成绩的茎叶图如图所示,则该生数学成绩在(135,140)内的概率为( )
重庆巴蜀中学高三的某位学生的10次数学考试成绩的茎叶图如图所示,则该生数学成绩在(135,140)内的概率为( )
 重庆巴蜀中学高三的某位学生的10次数学考试成绩的茎叶图如图所示,则该生数学成绩在(135,140)内的概率为( )
重庆巴蜀中学高三的某位学生的10次数学考试成绩的茎叶图如图所示,则该生数学成绩在(135,140)内的概率为( )| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
 如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.
如图,四边形ABCD是平行四边形,P是BD上任意一点,过P点的直线分别交AB,DC于E,F,交DA,BC的延长线于G,H.