题目内容
【题目】已知圆![]() :
: ![]() (其中
(其中![]() 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 作曲线
作曲线![]() 的切线交圆
的切线交圆![]() 于不同的两点
于不同的两点![]() (其中
(其中![]() 在
在![]() 的右侧),已知点
的右侧),已知点![]() .求四边形
.求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)曲线![]() 上任意一点
上任意一点![]() ,则
,则![]() 为
为![]() 上的点,从而可得曲线
上的点,从而可得曲线![]() 的方程为
的方程为![]() ,化简可得标准方程;(2),设
,化简可得标准方程;(2),设![]() ,由
,由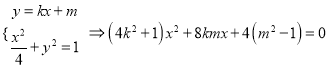 ,根据判别式为零可得
,根据判别式为零可得![]() ,根据韦达定理、弦长公式以及三角形面积公式可得
,根据韦达定理、弦长公式以及三角形面积公式可得![]() ,同理可得
,同理可得![]() ,则
,则![]() ,利用基本不等式可得四边形
,利用基本不等式可得四边形![]() 面积的最大值.
面积的最大值.
试题解析:(1)设曲线![]() 上任意一点
上任意一点![]() ,则
,则![]() 为
为![]() 上的点,
上的点,
![]() ,
, ![]() 曲线
曲线![]() 。
。
(2)易知直线![]() 的斜率
的斜率![]() 存在,设
存在,设![]() ,
,
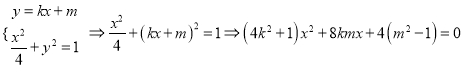 ,
,
![]() ,即
,即![]() ,
,
因为![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
则![]() ,
, ![]() ,
,
![]() ,
,
由![]() ,
,
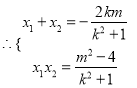 ,
,
![]() ,
,
![]() ,
,
![]()
而![]() ,
, ![]() ,易知
,易知![]() ,
, ![]() ,
,
 ,
, ![]() ,
,
![]() 。
。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】某机构通过对某企业今年的生产经营情况的调查,得到每月利润![]() (单位:万元)与相应月份数
(单位:万元)与相应月份数![]() 的部分数据如表:
的部分数据如表:
| 1 | 4 | 7 | 12 |
| 229 | 244 | 241 | 196 |
(1)根据如表数据,请从下列三个函数中选取一个恰当的函数描述![]() 与
与![]() 的变化关系,并说明理由,
的变化关系,并说明理由,![]() ,
,![]() ,
,![]() ;
;
(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.
【题目】《中华人民共和国个人所得税法》第十四条中有下表(部分):
个人所得税税率(工资、薪金所得适用)
级数 | 全月应纳所得额 | 税率(%) |
1 | 不超过 |
|
2 | 超过 |
|
3 | 超过 |
|
4 | 超过 |
|
5 | 超过 |
|
上表中“全月应纳税所得额”是从月工资、薪金收入中减去![]() 元后的余额.如果某人月工资、薪金收入为
元后的余额.如果某人月工资、薪金收入为![]() 元,那么他应纳的个人所得税为________元.
元,那么他应纳的个人所得税为________元.