题目内容
18.已知直线$l:\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\ y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.,(t为参数)$与圆$C:\left\{\begin{array}{l}x=1+\sqrt{2}cosθ\\ y=1+\sqrt{2}sinθ\end{array}\right.,(θ为参数)$,(1)求证:直线l与圆C相交;
(2)设直线l与圆C相交于A、B两点,又已知点P(m,0),m∈R,求||PA|-|PB||的最大值.
分析 (1)直线l消去参数t,得直线l的普通方程,圆C化为普通方程,求出圆心C到直线l:x+y-3=0的距离,由此能证明直线l与圆C相交.
(2)圆心坐标,直线l的方程求出AB长,当点P不在直线AB上,则这、A、B构成一个三角形,从而||PA|-|PB||<|AB|,当点P在直线AB上,||PA|-|PB||≤|AB|,由此能求出||PA|-|PB||的最大值.
解答  证明:(1)直线$l:\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\ y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.,(t为参数)$中,
证明:(1)直线$l:\left\{\begin{array}{l}x=1-\frac{{\sqrt{2}}}{2}t\\ y=2+\frac{{\sqrt{2}}}{2}t\end{array}\right.,(t为参数)$中,
消去参数t,得直线l的普通方程为x+y-3=0.
圆$C:\left\{\begin{array}{l}x=1+\sqrt{2}cosθ\\ y=1+\sqrt{2}sinθ\end{array}\right.,(θ为参数)$化为普通方程,
得:(x-1)2+(y-1)2=2,圆心C(1,1),半径r=$\sqrt{2}$,
圆心C(1,1)到直线l:x+y-3=0的距离:d=$\frac{|1+1-3|}{\sqrt{1+1}}$=$\frac{\sqrt{2}}{2}$$<r=\sqrt{2}$,
∴直线l与圆C相交.
解:(2)过圆心C作CD⊥AB,交AB于D,由(2)得CD=d=$\frac{\sqrt{2}}{2}$,
∴AB=2AD=2$\sqrt{{r}^{2}-C{D}^{2}}$=2$\sqrt{2-\frac{1}{2}}$=2×$\frac{\sqrt{6}}{2}$=$\sqrt{6}$.
当点P不在直线AB上,则这、A、B构成一个三角形,∴||PA|-|PB||<|AB|,
当点P在直线AB上,||PA|-|PB||≤|AB|=$\sqrt{6}$,
∴||PA|-|PB||的最大值为$\sqrt{6}$.
点评 本题考查直线与圆相交的证明,考查两线段之差的绝对值的最小值的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

| A. | 60° | B. | 90° | C. | 150° | D. | 120° |
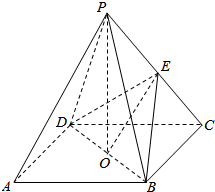 如图ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: 如图四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则以下四个结论:
如图四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则以下四个结论: