题目内容
6.x、y为正数,若2x+y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值为$3+2\sqrt{2}$.分析 由题意整体代入可得$\frac{1}{x}+\frac{1}{y}$=(2x+y)($\frac{1}{x}+\frac{1}{y}$)=3+$\frac{y}{x}$+$\frac{2x}{y}$,由基本不等式可得.
解答 解:∵正数x、y满足2x+y=1,
∴$\frac{1}{x}+\frac{1}{y}$=(2x+y)($\frac{1}{x}+\frac{1}{y}$)
=3+$\frac{y}{x}$+$\frac{2x}{y}$≥3+2$\sqrt{\frac{y}{x}•\frac{2x}{y}}$=$3+2\sqrt{2}$,
当且仅当$\frac{y}{x}$=$\frac{2x}{y}$即x=$\frac{2-\sqrt{2}}{2}$且y=$\sqrt{2}$-1时取等号.
故答案为:$3+2\sqrt{2}$
点评 本题考查基本不等式求最值,涉及“1”的整体代换,属基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
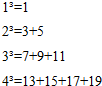 已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )
已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )