题目内容
(2013•闸北区二模)一个袋中装有大小相同的黑球、白球和红球共10个.已知从袋中任意摸出1个球,得到黑球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是
.从袋中任意摸出2个球,记得到白球的个数为ξ,则随机变量ξ的数学期望Eξ=
| 2 |
| 5 |
| 7 |
| 9 |
1
1
.分析:由条件从袋中任意摸出1个球,得到黑球的概率是
可得到黑球的个数;利用“从袋中任意摸出2个球,至少得到1个白球的”的对立事件“从袋中任意摸出2个球都不是白球”即可得出;由题意白球的个数随机变量ξ的取值为0,1,2,利用古典概型的概率计算公式和数学期望的计算公式即可得出Eξ.
| 2 |
| 5 |
解答:解:∵从袋中任意摸出1个球,得到黑球的概率是
,∴黑球的个数为10×
=4.
设白球的个数为x个,则红球的个数为6-x.设“从袋中任意摸出2个球,至少得到1个白球”为事件A,则其对立事件
为“从袋中任意摸出2个球都不是白球”,
由题意得P(A)=1-P(
)=1-
=
.解得x=5.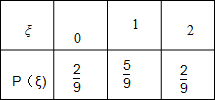
可知白球的个数为5个,则红球的个数为1个.
由题意白球的个数随机变量ξ的取值为0,1,2.
∴P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
.
随机变量ξ的分布列见右图
∴Eξ=0×
+1×
+2×
=1.
故答案为1.
| 2 |
| 5 |
| 2 |
| 5 |
设白球的个数为x个,则红球的个数为6-x.设“从袋中任意摸出2个球,至少得到1个白球”为事件A,则其对立事件
. |
| A |
由题意得P(A)=1-P(
. |
| A |
| ||
|
| 7 |
| 9 |

可知白球的个数为5个,则红球的个数为1个.
由题意白球的个数随机变量ξ的取值为0,1,2.
∴P(ξ=0)=
| ||
|
| 2 |
| 9 |
| ||||
|
| 5 |
| 9 |
| ||
|
| 2 |
| 9 |
随机变量ξ的分布列见右图
∴Eξ=0×
| 2 |
| 9 |
| 5 |
| 9 |
| 2 |
| 9 |
故答案为1.
点评:正确理解概率的意义、互为对立事件的概率之间的关系、古典概型的概率计算公式和数学期望计算公式是解题的关键.

练习册系列答案
相关题目