题目内容
若将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题,则该命题称为“可换命题”.下列四个命题:①垂直于同一平面的两直线平行;②垂直于同一平面的两平面平行;③平行于同一直线的两直线平行;④平行于同一平面的两直线平行.其中“可换命题”的是( )
| A.①② | B.① | C.①③ | D.③④ |
C
解析试题分析:垂直于同一直线的两直线可能平行,但也可能相交或异面,所以②不是“可换命题”;而平行于同一直线的两平面可能平行,但也可能相交,所以④不是“可换命题”.
考点:本小题主要考查空间中直线、平面的位置关系,考查逻辑推理能力和空间想象能力.
点评:准确灵活的运用定理,合理将已知条件转化为定理条件,并使用定理进行判是解这种类型题目的关键.

练习册系列答案
相关题目
设 是不同的直线,
是不同的直线, 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
① ②
② ③
③ ④
④
其中正确的个数( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设 为三条不同的直线,
为三条不同的直线, 为一个平面,下列命题中不正确的是( )
为一个平面,下列命题中不正确的是( )
A.若 ,则 ,则 与 与 相交 相交 |
B.若 则 则 |
C.若  // //  , , // //  , , ,则 ,则 |
D.若 // //  , , , , ,则 ,则 // //  |
关于直线a,b,c以及平面M,N,给出下面命题:
①若a//M,b//M, 则a//b ②若a//M, b⊥M,则b⊥a ③若a M,b
M,b M,且c⊥a,c⊥b,则c⊥M ④若a⊥M, a//N,则M⊥N,其中正确命题的个数为( )
M,且c⊥a,c⊥b,则c⊥M ④若a⊥M, a//N,则M⊥N,其中正确命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
垂直于同一平面的两条直线一定( )
| A.相交 | B.平行 | C.异面 | D.以上都有可能 |
已知 和
和 是两条不同的直线,
是两条不同的直线, 和
和 是两个不重合的平面,那么下面给出的条件中一定能推出
是两个不重合的平面,那么下面给出的条件中一定能推出
 的是( )
的是( )
A. ,且 ,且 | B. ∥ ∥ ,且 ,且  |
C. ,且 ,且 ∥ ∥ | D.  ,且 ,且 ∥ ∥ |
如图,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AB1、BC1的中点,则以下结论中不成立的是( )
| A.EF与BB1垂直 | B.EF与BD垂直 |
| C.EF与CD异面 | D.EF与A1C1异面 |
 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 是
是 的中点,则
的中点,则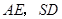 所成的角的余弦值为( )
所成的角的余弦值为( )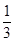



 中,底面正方形
中,底面正方形 的边长为1,侧棱长为2,则异面直线
的边长为1,侧棱长为2,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )