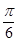题目内容
设 为三条不同的直线,
为三条不同的直线, 为一个平面,下列命题中不正确的是( )
为一个平面,下列命题中不正确的是( )
A.若 ,则 ,则 与 与 相交 相交 |
B.若 则 则 |
C.若  // //  , , // //  , , ,则 ,则 |
D.若 // //  , , , , ,则 ,则 // //  |
B
解析试题分析: 因为A.若 ,则利用线面垂直的定义可知,则
,则利用线面垂直的定义可知,则 与
与 相交 成立。
相交 成立。
B.若 则
则 ,只有m,n相交时成立,选项B错误。
,只有m,n相交时成立,选项B错误。
C.若  //
//  ,
, //
//  ,
, ,因为利用平行的传递性可知,l//n,则根据平行线中一条垂直于这个平面,则另一条也垂直于该平面,故
,因为利用平行的传递性可知,l//n,则根据平行线中一条垂直于这个平面,则另一条也垂直于该平面,故 成立。
成立。
D.若 //
//  ,
, ,
, ,则根据线面垂直的性质定理可知,m//n,
,则根据线面垂直的性质定理可知,m//n,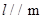 ,根据平行的传递性得到结论,故
,根据平行的传递性得到结论,故 //
//  成立。故选B.
成立。故选B.
考点:本题主要考查了立体几何中线面的位置关系的判定和运用。
点评:解决该试题的关键是熟练的掌握空间中点、线、面的位置关系的运用。尤其是垂直的判定定理和平行判定定理的问题,要注意严密性。

练习册系列答案
相关题目
如图,长方体ABCD-A1B1C1D1中,AB=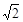 ,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )
,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )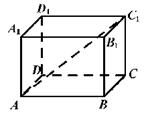
| A.30° | B.45° | C.60° | D.90° |
已知二面角 是直二面角,P为棱AB上一点,PQ、PR分别在平面
是直二面角,P为棱AB上一点,PQ、PR分别在平面 、
、 内,且
内,且 ,则
,则 为( )
为( )
| A.45° | B.60° | C.120° | D.150° |
若将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题,则该命题称为“可换命题”.下列四个命题:①垂直于同一平面的两直线平行;②垂直于同一平面的两平面平行;③平行于同一直线的两直线平行;④平行于同一平面的两直线平行.其中“可换命题”的是( )
| A.①② | B.① | C.①③ | D.③④ |
设m、n是两条不同的直线, 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若 ,
, ,则
,则 ②若
②若 ,
, ,
, ,则
,则
③若 ,
, ,则
,则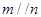 ④若
④若 ,
, ,则
,则
其中正确命题的序号是 ( )
| A.②和③ | B.①和② | C.③和④ | D.①和④ |
 在正方体
在正方体 的对角线
的对角线 上.过点
上.过点 的直线,与正方体表面相交于
的直线,与正方体表面相交于 设
设 则函数
则函数 的图象大致是( )
的图象大致是( )
 ,且PA,PB,PC两两垂直,则P到面ABC的距离为( )
,且PA,PB,PC两两垂直,则P到面ABC的距离为( )

 ,E为侧棱PC的中点,则PA与BE所成的角为( )
,E为侧棱PC的中点,则PA与BE所成的角为( )