题目内容
【题目】极坐标系的极点在平面直角坐标系的原点O处,极轴与x轴的正半轴重合,两坐标系单位长度相同.已知曲线的极坐标方程为ρ=2cosθ+2sinθ,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(Ⅰ)将直线l的参数方程化为普通方程,将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设曲线C上到直线l的距离为d的点的个数为f(d),求f(d)的解析式.
【答案】解:(Ⅰ)直线l的参数方程为 ![]() (t为参数),消去参数,可得普通方程x+y﹣1=0;
(t为参数),消去参数,可得普通方程x+y﹣1=0;
曲线的极坐标方程为ρ=2cosθ+2sinθ,即ρ2=2ρcosθ+2ρsinθ,∴x2+y2﹣2x﹣2y=0;
(Ⅱ)x2+y2﹣2x﹣2y=0,可化为(x﹣1)2+(y﹣1)2=2,
圆心C(1,1)到直线l的距离为 ![]() =
= ![]() ,圆的半径为
,圆的半径为 ![]() ,
,
圆上的点到直线l距离d的取值范围是0≤d≤ ![]()
∴f(d)= 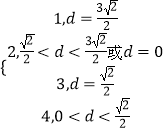
【解析】(Ⅰ)将直线l的参数方程消去参数,可得普通方程,将曲线C的极坐标方程,即ρ2=2ρcosθ+2ρsinθ,即可化为直角坐标方程;(Ⅱ)圆心C(1,1)到直线l的距离为 ![]() =
= ![]() ,圆的半径为
,圆的半径为 ![]() ,圆上的点到直线l距离d的取值范围是0≤d≤
,圆上的点到直线l距离d的取值范围是0≤d≤ ![]() ,即可求f(d)的解析式.
,即可求f(d)的解析式.

练习册系列答案
相关题目
【题目】某地区10名健康儿童头发和血液中的硒含量(单位:μg/ml)如下表所示:
血硒x | 74 | 66 | 88 | 69 | 91 | 73 | 66 | 96 | 58 | 73 |
发硒y | 13 | 10 | 13 | 11 | 16 | 9 | 7 | 14 | 5 | 10 |
(1)画出散点图;
(2)求回归方程;
(3)若某名健康儿童的血液中的硒含量为94 μg/ml,预测他的发硒含量.

