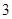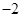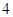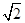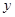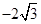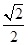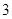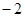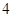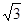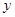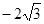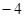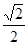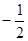题目内容
设椭圆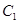 与抛物线
与抛物线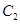 的焦点均在
的焦点均在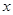 轴上,
轴上,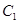 的中心及
的中心及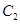 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)求曲线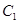 、
、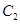 的标准方程;
的标准方程;
(Ⅱ)设直线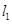 过抛物线
过抛物线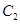 的焦点
的焦点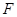 ,
,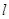 与椭圆交于不同的两点
与椭圆交于不同的两点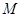 、
、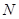 ,当
,当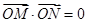 时,求直线
时,求直线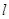 的方程.
的方程.
【答案】
(1)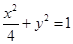 ,
,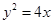
(2)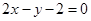 或
或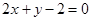
【解析】
试题分析:解(1)由椭圆标准方程及抛物线标准方程可得出
点(-2,0)、(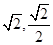 )是椭圆上两点
)是椭圆上两点
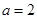


椭圆标准方程 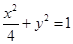
由点(3,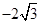 )、(4,-4)抛物线开口向右,其方程
)、(4,-4)抛物线开口向右,其方程
12=6P
P=2 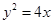 4分
4分
(II)抛物焦点坐标F(1,0)
若直线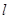 垂直于
垂直于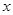 轴,方程
轴,方程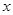 =1,由
=1,由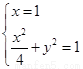 解故 M(1,
解故 M(1, ),N(1,
),N(1, )
)
 ∴
∴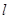 与
与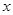 轴不垂直
轴不垂直
设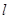 方程
方程 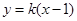
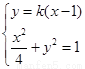 消去
消去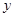 得:
得: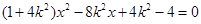
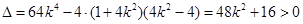
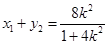
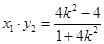

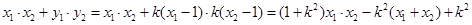
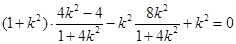
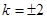
直线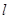 的方程
的方程 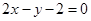 或
或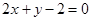 12分
12分
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
已知F1、F2分别为椭圆C1:
+
=1(a>b>0)的左右焦点,抛物线C2以F1为顶点,F2为焦点,设P是椭圆与抛物线的一个交点,如果椭圆的离心率e满足|PF1|=e|PF2|,则e=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、2-
| ||||
B、
| ||||
C、
| ||||
D、2-
|
已知F1、F2为椭圆E的左右两个焦点,抛物线C以F1为顶点,F2为焦点,设P为椭圆与抛物线的一个交点,如果椭圆离心率为e,且|PF1|=e|PF2|则e的值为( )
A、
| ||||
B、2-
| ||||
C、
| ||||
D、2-
|
(本小题满分14分)设椭圆 与抛物线
与抛物线 的焦点均在
的焦点均在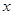 轴上,
轴上, 的中心和
的中心和 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)求 ,
, 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率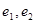 ;
;
2)设直线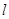 与椭圆
与椭圆 交于不同的两点
交于不同的两点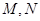 ,且
,且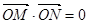 (其中
(其中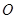 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线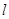 过抛物线
过抛物线 的焦点
的焦点 若存在,求出直线
若存在,求出直线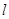 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.