题目内容
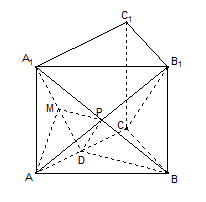
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是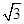 ,D是AC的中点.
,D是AC的中点.

(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值.
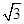 ,D是AC的中点.
,D是AC的中点.
(1)求证:B1C∥平面A1BD;
(2)求二面角A1-BD-A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值.
(1)详见解析;(2)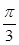 ;(3)
;(3)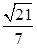 .
.
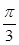 ;(3)
;(3)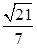 .
.试题分析:(1)设AB1与A1B相交于点P,连接PD,则P为AB1中点,根据中位线定理可知PD∥B1C,
根据线面平行即可得证;(2)由于AA1⊥底面ABC,且BD⊥AC,所以A1D⊥BD,可知∠A1DA就是二面角A1-BD-A的平面角,在三角形A1DA 中,tan∠A1DA=
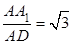 ,即可求出二面角的平面角为
,即可求出二面角的平面角为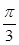 ,即可求出二面角;(3)由(2)作AM⊥A1D,M为垂足,由于BD⊥AC,平面A1ACC1⊥平面ABC,可证BD⊥平面A1ACC1,即可BD⊥AM,可证明AM⊥平面A1DB,连接MP,可知∠APM就是直线A1B与平面A1BD所成的角,在Rt△AA1D中就可以求出∠APM的正弦值,进而求出结果.
,即可求出二面角;(3)由(2)作AM⊥A1D,M为垂足,由于BD⊥AC,平面A1ACC1⊥平面ABC,可证BD⊥平面A1ACC1,即可BD⊥AM,可证明AM⊥平面A1DB,连接MP,可知∠APM就是直线A1B与平面A1BD所成的角,在Rt△AA1D中就可以求出∠APM的正弦值,进而求出结果.解:(1)设AB1与A1B相交于点P,连接PD,则P为AB1中点,
∵D为AC中点,∴PD∥B1C,
又∵PD
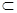 平面A1BD,∴B1C∥平面A1BD;
平面A1BD,∴B1C∥平面A1BD;(2)∵正三棱住ABC-A1B1C1,∴AA1⊥底面ABC,
又∵BD⊥AC,∴A1D⊥BD,∴∠A1DA就是二面角A1-BD-A的平面角,
∵AA1=
 ,AD=
,AD=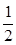 AC=1,∴tan∠A1DA=
AC=1,∴tan∠A1DA=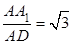 ,∴∠A1DA=
,∴∠A1DA=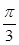 ,即二面角A1-BD-A的大小是
,即二面角A1-BD-A的大小是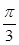 ;
;(3)由(2)作AM⊥A1D,M为垂足,
∵BD⊥AC,平面A1ACC1⊥平面ABC,平面A1ACC1∩平面ABC=AC,∴BD⊥平面A1ACC1,
∵AM
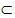 平面A1ACC1,∴BD⊥AM,
平面A1ACC1,∴BD⊥AM,∵A1D∩BD=D,∴AM⊥平面A1DB,连接MP,
则∠APM就是直线A1B与平面A1BD所成的角,
∵AA1=
 ,AD=1,∴在Rt△AA1D中,∠A1DA=
,AD=1,∴在Rt△AA1D中,∠A1DA=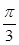 ,∴AM=1×sin60°=
,∴AM=1×sin60°= ,AP=
,AP=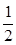 AB1=
AB1=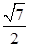 ,∴sin∠APM=
,∴sin∠APM=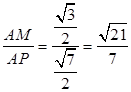 ,∴直线AB1与平面A1BD所成的角的正弦值为
,∴直线AB1与平面A1BD所成的角的正弦值为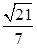 .
. 

练习册系列答案
相关题目
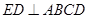 ,ED=1,
,ED=1,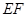 //BD,且
//BD,且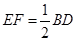 .
.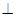 平面BDEF;
平面BDEF;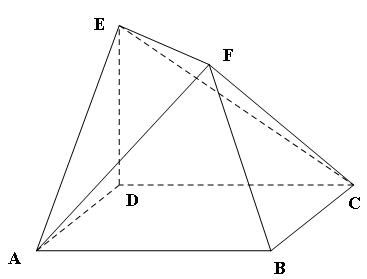
 中,
中, ,
, ,D、E分别是
,D、E分别是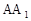 、
、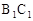 的中点,
的中点,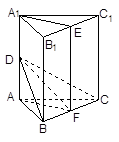
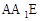 ⊥面BCD;
⊥面BCD;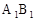 与平面BCD所成的角.
与平面BCD所成的角.
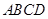 是菱形,
是菱形,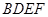 是矩形,
是矩形,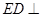 面
面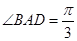 .
.
 ;
;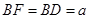 ,求四棱锥
,求四棱锥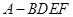 的体积.
的体积.
 ;②一定存在平行于a的平面
;②一定存在平行于a的平面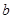 ∥
∥ ;④一定存在无数个平行于a的平面
;④一定存在无数个平行于a的平面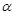 、
、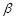 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( )