Question

【题目】已知函数f（x）= ， ①若f（a）=14，求a的值
②在平面直角坐标系中，作出函数y=f（x）的草图．（需标注函数图象与坐标轴交点处所表示的实数）

Answer 1

【答案】解：①∵函数f（x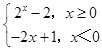）= ，f（a）=14，

当a≥0时，由f（a）=2a﹣2=14，求得a=4；

当a＜0时，由f（a）=1﹣2a=14，求得a=﹣ ．

综上可得，a=4或a=﹣ ．

②当x≥0时，把函数y=2x的图象向下平移2个单位，

可得f（x）的图象；

当x＜0时，作出函数y=1﹣2x的图象即可得到f（x）的图象．

在平面直角坐标系中，作出函数y=f（x）的草图，如图所示：

【解析】①分当a≥0时和当a＜0时2种情况，分别根据f（a）=14，求得a的值．②分当x≥0时和当x＜0时2种情况，分别作出函数f（x）的图象．
【考点精析】掌握函数的图象是解答本题的根本，需要知道函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值．