题目内容
点P是直线l：x-y-2=0上的动点，点A，B分别是圆C1：（x+3）2+（y-1）2=4和圆C2：x2+（y-3）2=1上的两个动点，则|PA|+|PB|的最小值为______．
设圆C'是圆C2：x2+（y-3）2=1关于直线l对称的圆
可得C'（5，-2），圆C'方程为（x-5）2+（y+2）2=1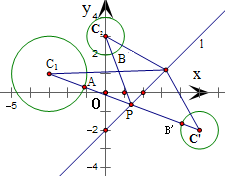
可得当点P位于线段C1C'上时，线段AB'长是圆C1与圆C'上两个动点之间的距离最小值
B'关于直线l对称的点在圆C2上，由平几知识得当圆C2上的
动点B与该点重合时，|PA|+|PB|达到最小值
∵|C1C'|=
=
，
可得|AB'|=|C1C'|-r1-r2=
-3
因此，|PA|+|PB|的最小值等于|AB'|=
-3
故答案为：
-3
可得C'（5，-2），圆C'方程为（x-5）2+（y+2）2=1
可得当点P位于线段C1C'上时，线段AB'长是圆C1与圆C'上两个动点之间的距离最小值
B'关于直线l对称的点在圆C2上，由平几知识得当圆C2上的
动点B与该点重合时，|PA|+|PB|达到最小值
∵|C1C'|=
| (5+3)2+(-2-1)2 |
| 73 |
可得|AB'|=|C1C'|-r1-r2=
| 73 |
因此，|PA|+|PB|的最小值等于|AB'|=
| 73 |
故答案为：
| 73 |
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
