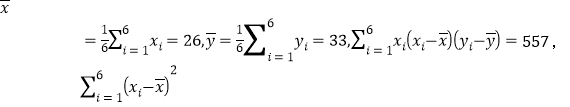题目内容
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,其离心率
,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值为3.
面积的最大值为3.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,过点
,过点![]() 且斜率不为0的直线
且斜率不为0的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,直线
两点,直线![]() ,
,![]() 与
与![]() 轴分别相交于
轴分别相交于![]() 两点,试问
两点,试问![]() 是否为定值?如果,求出这个定值;如果不是,请说明理由.
是否为定值?如果,求出这个定值;如果不是,请说明理由.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:
(1)由题意得到关于b,c的方程组,求解方程组结合椭圆的性质可得![]() ,则椭圆
,则椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设直线![]() 的y轴截距式方程:
的y轴截距式方程:![]() ,结合直线方程可得
,结合直线方程可得![]() ,
,![]() . 联立直线方程与椭圆方程有
. 联立直线方程与椭圆方程有![]() ,结合韦达定理可得
,结合韦达定理可得![]() ,则
,则![]() 为定值.
为定值.
试题解析:
(1)由题意知,当点![]() 是椭圆的上、下顶点时,
是椭圆的上、下顶点时,![]() 的面积最大,
的面积最大,
此时![]() 的面积
的面积![]() ,①
,①
又椭圆的离心率![]() ,②
,②
由①②得:![]() ,
,
所以,椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,则
,则
直线![]() 的方程为
的方程为![]() ,则
,则![]() ,即
,即![]() ,
,
同理可得![]() .
.
由![]() 得
得![]() ,
,
由![]() 得
得![]() 且
且![]() ,
,
所以![]()
 ,
,
故![]() 为定值
为定值![]() .
.

练习册系列答案
相关题目
【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 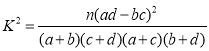 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |