题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() (
(![]() )的左焦点为
)的左焦点为![]() ,且点
,且点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 同时与椭圆
同时与椭圆![]() 和抛物线
和抛物线![]() :
:![]() 相切,求直线
相切,求直线![]() 的方程.
的方程.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]()
【解析】
试题分析:(1)因为椭圆![]() 的左焦点为
的左焦点为![]() ,所以c=1,点P(0,1)代入椭圆
,所以c=1,点P(0,1)代入椭圆![]() ,得b=1,由此求出椭圆
,得b=1,由此求出椭圆![]() 的方程;(2)设直线l的为y=kx+m,由
的方程;(2)设直线l的为y=kx+m,由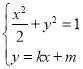 得
得![]() .因为直线l与椭圆
.因为直线l与椭圆![]() 相切,所以
相切,所以![]() .由此能求出直线l的方程
.由此能求出直线l的方程
试题解析:(1)因为椭圆![]() 的左焦点为
的左焦点为![]() ,所以
,所以![]() ,
,
点![]() 代入椭圆
代入椭圆![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)直线![]() 的斜率显然存在,设直线
的斜率显然存在,设直线![]() 的方程为
的方程为![]() ,
,
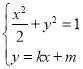 ,消去
,消去![]() 并整理得
并整理得![]() ,
,
因为直线![]() 与椭圆
与椭圆![]() 相切,所以
相切,所以![]() ,
,
整理得![]() ①
①
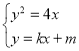 ,消去
,消去![]() 并整理得
并整理得![]() 。
。
因为直线![]() 与抛物线
与抛物线![]() 相切,所以
相切,所以![]() ,
,
整理得![]() ②
②
综合①②,解得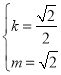 或
或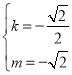 。
。
所以直线![]() 的方程为
的方程为![]() 或
或![]()

练习册系列答案
相关题目